How to map and sum a list fast?

Question

The following takes a lot of memory and is slow:

AbsoluteTiming[Total[Map[#^2 &, Range[1, 100000000]]]]

I suspect this is because it first calculates and stores the whole list of squared numbers and then performs the summation. At least it would try it, if it wasn't running out of memory (8GB on ubuntu).

On the other hand, Haskell with its lazy evaluation can calculate this:

Prelude Data.List> :set +s
Prelude Data.List> foldl' (+) 0 $ map (\x -> x^2) [1..100000000]
333333338333333350000000
(60.08 secs, 74,975,662,856 bytes)

It is slow (a whole minute), since this is the interpreter with no optimization, but at least it runs in a constant memory and yields a result.

I am quite sure a couple of years ago I knew the solution, but I forgot.

Answer 1

AbsoluteTiming[Total[Range[1, 100000000]^2]]
(* {26.0686, 333333338333333350000000} *)

or

AbsoluteTiming[#.# &@Range[1, 100000000]]
(* {35.2883, 333333338333333350000000} *)

or

AbsoluteTiming@Total[Range[1, 100000000] /. {x_ -> x^2}]
(* {30.9893, 333333338333333350000000} *)

To compare with @corey979 solution

out = 0;
Do[out = out + i^2, {i, 1, 100000000}]; // AbsoluteTiming
(* {95.0359, Null} *)

And the winner is ... :)

s2[n_] := Sum[i^2, {i, 1, n}]
AbsoluteTiming@s2[100000000]
(* {0.003762, 333333338333333350000000} *)

Seriously though, the OP's solution is not that slow at all:

AbsoluteTiming[Total[Map[#^2 &, Range[1, 100000000]]]]
(* {27.5232, 333333338333333350000000} *)

And to imitate Haskell way:

AbsoluteTiming@Fold[#1 + #2^2 &, 0, Range[1, 100000000]]
(* {113.901, 333333338333333350000000} *)

And to summarize all above, we can have a naive benchmark:

d[n_] := First@AbsoluteTiming[#.# &@Range[n]];
t[n_] := First@AbsoluteTiming[Total[Range[n]^2]];
op[n_] := First@AbsoluteTiming@Total[Map[#^2 &, Range[n]]];
re[n_] := First@AbsoluteTiming@Total[Range[n] /. {x_ -> x^2}];
range = {#, 3 #} & /@ (10^Range[3, 7, 1]) // Flatten;
flist = {d, t, op,re};
data = Table[{n, #[n]}, {n, range}] & /@ flist;
ListLogLogPlot[data, PlotLegends -> flist, AxesLabel -> {n, Time}, 
 GridLines -> Automatic]

So the d[n] and t[n] were good up to 3 million and the Dot is the fastest up to 1 million.

Edit

As @Alan noticed in comments, s2[n] behaves strangely. Here is a separate plot for s2

It looks like it actually does summation for small $n$ and then starts using formula ~ $10^6$, so time drops significantly. There is also a jump when $n$ reaches 10^11 but this time the time increases, I guess it's due to the fact that numbers are too big for standard CPU multiplications of integers.

Answer 2

To overcome the memory issues, let's store as few data in the memory as possible:

out = 0;
Do[out = out + i^2, {i, 1, 100000000}]; // AbsoluteTiming
out

{58.7571, Null}

333333338333333350000000

I observed 100-200 MB memory usage in the system monitor.

For comparison, the original approach from OP's question:

AbsoluteTiming[Total[Map[#^2 &, Range[1, 100000000]]]]

{11.2087, 333333338333333350000000}

and it ate 5.6 GB of memory.

---

EDIT: Using the parallelized version from Karsten 7.'s answer I got the result on a 4 core machine in 17.098 seconds - i.e., 3.44 times faster. I'd expect the parallelized Do loop to be faster than the OP's approach on an 8 core machine (not so rare these days). On a $\geq 16$ core cluster the benefit from parallelization would be significant.

Moreover, while BlacKow's thorough analysis takes advantage of the structure of the data, in case when the data are e.g. experimental and no such clear pattern is observed, a parallelized Do loop might be the most efficient way to handle them.

When memory is crucial, thanks to an analysis of Eric Towers, it appears that Do is the most efficient solution. When it's parallelized, it can also compete when it comes to timing.

---

EDIT 2: I don't fully reproduce the behaviour of BlacKow's s2 timing:

---

EDIT 3: The best option to compute the sum of squares really fast is to do

s2[n_] := Sum[i^2, {i, 1, n}]
s2[a]

1/6 a (1 + a) (1 + 2 a)

sum[a_] := 1/6 a (1 + a) (1 + 2 a)

sum2[n_] := First @ AbsoluteTiming[sum[#]& @ n];

range = {#, 3 #}& /@ (10^Range[1, 20, 1]) // Flatten;
flist = {sum2};
data = Table[{n, #[n]}, {n, range}]& /@ flist;
ListLogLogPlot[data, PlotLegends -> flist, AxesLabel -> {n, Time}, 
 GridLines -> Automatic]

:P

Answer 3

This addresses the underlying problem, which implies a really fast way is not likely to be found, and shows yet another way to sum a list, Tr.

One reason the OP's sum is slow is that the sum is bigger than a machine integer (which is what I think BlacKow was guessing). Even the little difference of a few hundred terms makes a big difference in time:

Tr[Range[1, 3024600]^2] // Internal`PositiveMachineIntegerQ
Tr[Range[1, 3025000]^2] // Internal`PositiveMachineIntegerQ
(*
  True
  False
*)

AbsoluteTiming[Tr[Range[1, 3024600]^2]]
AbsoluteTiming[Tr[Range[1, 3025000]^2]]
(*
  {0.018311, 9223225016415084100}
  {0.604474, 9226884783646337500}
*)

On machine reals, the sum is much faster,

AbsoluteTiming[Tr[Range[1., 100000000]^2]]
(*  {0.758036, 3.33333*10^23}  *)

although the OP's code is not so much faster,

AbsoluteTiming[Total[Map[#^2 &, Range[1., 100000000]]]]
(*  {3.76371, 3.33333*10^23}  *)

As for memory usage, corey's Do[] loop is probably closest to Haskell's lazy version of Fold.

Answer 4

Since OP's core complaint appears to be about memory use, I've generated memory usage statistics to match BlacKow's data:

d[n_]  := #.# &@Range[n];
t[n_]  := Total[Range[n]^2];
op[n_] := Total[Map[#^2 &, Range[n]]];
re[n_] := Total[Range[n] /. {x_ -> x^2}];
s2[n_] := Sum[i^2, {i, 1, n}];

memUsed[f_, n_] := Module[{
  low, mid, up,
  try
  },
  up = 2^0;
  While[
    MemoryConstrained[f[n], up] === $Aborted,
    up *= 2;
  ];  (* So f[n] requires somewhere in (up/2, up] bytes.  *)

  low = up/2;
  While[up - low > 1,
    mid = 1/2 (up + low);
    try = MemoryConstrained[f[n], mid];
    (*Print[{low,up}, "\t", mid,"\t", try];*)
    If[try === $Aborted,
      low = mid,
      up = mid;
    ];
  ];
up]

memUsed[] performs an unbounded binary search to find the memory usage. It is noteworthy that memUsed[] results are not stable on multiple calls.

memUsed[op, 10^6]
memUsed[op, 10^6]
memUsed[op, 10^6]
(*  24 000 768  *)
(*  24 000 648  *)
(*  24 000 920  *)

Perhaps they're "stable enough".

range = {#, 3 #} & /@ (10^Range[3, 7, 1]) // Flatten;
flist = {d, t, op, re, s2};
data = Table[{n, memUsed[#, n]}, {n, range}] & /@ flist;
ListLogLogPlot[data, PlotLegends -> flist, AxesLabel -> {n, "Memory"},
  GridLines -> Automatic]

For your original range, I get

memUsed[op, 10^8]
(*  6 400 000 224  *)

6+ GB could be a bit difficult to acquire in an 8 GB environment (depending on what else the computer was doing and whether M'ma requested this memory in large allocations or lots of small ones).

Edit

Expanded to include Michael E2's Tr method and corey979's Do method as well as a probably irrelevant variant.

Clear[d, t, op, re, s2, tr, do1, do2];
d[n_] := #.# &@Range[n];
t[n_] := Total[Range[n]^2];
op[n_] := Total[Map[#^2 &, Range[n]]];
re[n_] := Total[Range[n] /. {x_ -> x^2}];
s2[n_] := Sum[i^2, {i, 1, n}];
tr[n_] := Tr[Range[1, n]^2];  (* Michael E2's *)
do1[n_] := (out = 0; Do[out = out + i^2, {i, 1, n}]; out) (* corey979's *)
do2[n_] := (out = 0; Do[out += i^2, {i, 1, n}]; out);

range = {#, 3 #} & /@ (10^Range[3, 7, 1]) // Flatten;
flist = {d, t, op, re, s2, tr, do1, do2};
data = Table[{n, memUsed[#, n]}, {n, range}] & /@ flist;
ListLogLogPlot[data, PlotLegends -> flist, AxesLabel -> {n, "Memory"},
  GridLines -> Automatic]

I'm not convinced the differences between do1 and do2 are meaningful.

Answer 5

Between fast, but memory hungry, vectorized operations represented by Total[Range[10^8]^2] and slow, but memory efficient, top level iteration represented by Do solution, there's a middle ground. One can generate data in chunks of specified length and use vectorized operations on those chunks. This way you can get constant memory usage dictated by size of a chunk and still have reasonable speed thanks to vectorized operations.

Until Streaming` module, that introduces general framework for such operations, is finished and documented, we can implement simple "folding in chunks" by hand.

ClearAll[chunkFold]
chunkFold[f_, x_, {min_Integer?Positive, max_Integer?Positive, chunkSize_Integer?Positive, getChunk_}] /; min <= max :=
    Module[{result = x, i},
        Do[
            result = f[result, getChunk[i , i + chunkSize - 1]],
            {i, min, max - chunkSize, chunkSize}
        ];
        f[result, getChunk[min + Quotient[max - min, chunkSize] chunkSize, max]]
    ]

chunkFold function folds given function f over subsequent "chunks" of data generated by getChunk function. getChunk[i, j] should give list of elements with indices from i to j. In total function uses indices from min to max in chunks of given chunkSize. Example of "symbolic" usage:

chunkFold[f, x, {3, 20, 5, getChunk}]
(* f[f[f[f[x, getChunk[3, 7]], getChunk[8, 12]], getChunk[13, 17]], getChunk[18, 20]] *)

In some problems, like one in OP, chunk size can be used not only to control memory usage, but also to limit size of intermediate results, that can decide whether it's enough to use machine numbers and packed arrays, or whether non-machine numbers must be used.

---

Let's define simple helper function, giving timing and memory usage together with result of evaluation of given expression:

timeMem = Function[,
    Module[{result}, Prepend[AbsoluteTiming@MaxMemoryUsed[result = #], result]],
    HoldFirst
];

Now let's use our chunkFold function for problem from OP:

chunkFold[#1 + Tr@Power[#2, 2] &, 0, {1, 10^8, 900, Range}] // timeMem
(* {333333338333333350000000, 0.969158, 18024} *)

result is calculated in one second using 18 kilobytes of memory. Which can be compared to simple Do, looping trough individual elements:

Module[{out = 0, i}, Do[out += i^2, {i, 10^8}]; out] // timeMem
(* {333333338333333350000000, 58.9343, 1112} *)

that uses one minute and one kilobyte.

---

Let's check how speed and memory usage of different solutions depends on total number of elements. We'll test three functions: do is simple iteration over every element, trPower is fully vectorized, trPowerChunk is intermediate solution using vectorized functions on chunks of 900 elements.

do[n_] := Module[{out = 0, i}, Do[out += i^2, {i, n}]; out]
trPower[n_] := Tr[Range[1, n]^2]
trPowerChunk[n_] := chunkFold[#1 + Tr@Power[#2, 2] &, 0, {1, n, 900, Range}]

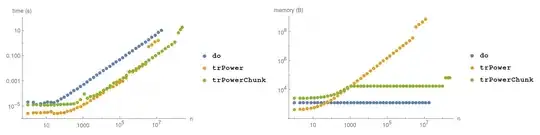
We see that do is slowest, but has constant, lowest, usage of memory.

trPower is fastest up to around 3*10^6, when as explained by Michael E2 numbers become to large to be stored as machine integers and Mathematica starts unpacking lists. Memory usage is proportional to number of elements, with larger proportionality constant after unpacking starts.

trPowerChunk is almost as fast as trPower before the latter starts unpacking, and fastest afterward. Memory usage of trPowerChunk grows up to n = 900, which was chosen as chunk size, and is constant afterward. From 101176707 sum of squares of consecutive 900 integers is larger than largest machine integer, so Mathematica starts unpacking arrays and we see jump in both time and memory usage. Memory usage is still constant, after unpacking, but this constant is higher.

Answer 6

ParallelSum[i^2, {i, 100000000}, Method -> "CoarsestGrained"] // AbsoluteTiming

{0.128204, 333333338333333350000000}

---

The parallelized version of the Do loop in the answer by corey979:

AbsoluteTiming[
 ParallelEvaluate[out = 0];
 ParallelDo[out += i^2, {i, 100000000}];
 Total@ParallelEvaluate[out]
 ]

{35.3163, 333333338333333350000000}

Answer 7

I don't know why I missed this question, but the Streaming` framework computes this out of the box. Unfortunately, it has to be patched in modern versions of Mathematica, so I refer to this answer for a patch. Assuming that that code has been executed, let us create a lazy range:

lr = Streaming`ListAPI`Lazy`LazyRange[1, 100000000]

Then check its length:

Length @ lr

(* 100000000 *)

And finally:

AbsoluteTiming[Total[Map[#^2 &, lr]]]

(* {18.63, 333333338333333350000000}  *)

and

MaxMemoryUsed[]

(* 236753504 *)

Answer 8

using NSum, the totoal timing is pretty fast, and you can even calculate larger numbers without memory issues.

    AbsoluteTiming@NSum[i^2, {i, 1, 100000000}]

{0.003697, 3.33333*10^23}
```