Solve integro differential equation numerically

Question

I want to solve the following equation numerically:

with initial condition y[0]=0 and y'[0]=0

I tried to do so by using the NDSolve function:

eqn = Derivative[2][y][x] == 1+y[x] - Integrate[Derivative[1][y][x - t]/sqrt[t], {t, 0, x}]; NDSolve[{eqn, y[0] == 0, Derivative[1][y][0] == 0}, y, {x, 0, 1}]

But it seems like Matlab cannot solve it directly. Do you have any suggestions?

Answer 1

As mentioned in the comment above, sqrt should be Sqrt and Matlab should be Mathematica, these aren't the main issue here of course. Currently NDSolve can't handle the problem, but we can solve the equation with the help of LaplaceTransform:

teqn = LaplaceTransform[eqn, x, s] /. Rule @@@ ic
tsol = Solve[teqn, LaplaceTransform[y[x], x, s]][[1, 1, -1]]
(* 1/(s (-1 + Sqrt[\[Pi]] Sqrt[s] + s^2)) *)

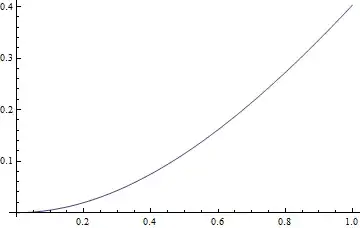
InverseLaplaceTransform can't handle tsol, so I turned to this numeric Laplace inversion package:

Plot[FT[(s \[Function] #) &@tsol, x], {x, 0, 1}]

Finally, DSolve in v11 can solve this equation in principle, but sadly it doesn't give the correct answer in this case, I think there's no doubt it's a bug:

eqn = y''[x] == 1 + y[x] - Integrate[y'[x - t]/Sqrt[t], {t, 0, x}];

ic = {y[0] == 0, y'[0] == 0};

sol[x_] = y[x]/.First@DSolve[{eqn, ic}, y@x, x]
(* 1/2 E^-x (-1 + E^x)^2 *)
Plot[{sol@x, FT[(s \[Function] #) &@tsol, x]}, {x, 0, 1}, 
 PlotLegends -> {"Output of DSolve", "Numeric Solution"}]

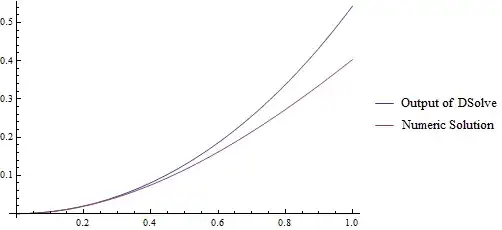
What's more awkward is, if the second argument of DSolve is modified to y i.e. if we write DSolve[{eqn, ic}, y, x], DSolve will return the input... Seems that this new feature is still unstable.