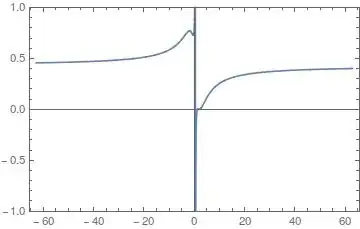
So I need to "define and plot on an appropriate interval":
f[x_]=(3x^3-16x^2+28X-16)/(7x^3-9x^2+48x-20)
to see the behavior of the function. The above function, however, doesn't work. My Calculus professor, in his boundless wisdom, made a function where the x variables will simply cancel out. I'm not sure what to do for a workaround, so I've been substituting x==2.
When I try to plot this function
Plot[f[2], {x, -20Pi, 20Pi}]
I receive a blank graph. How do I make Mathematica draw the function? (or just a line, I'll settle for anything at this point.)
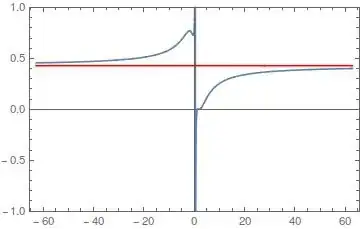
Later on I do have to "Plot the function and the horizontal line it approaches as x->Infinity on one graph" using the same function, so I'm hoping to eliminate the same potential problem for that as well.