Adding points limits

Question

With 4 points I set a path where your total length was subdivided into 300 points

Clear["Global`*"]  
points={{0,0},{5,8.07774721},{10,4.24499363},{20,9.28880172}}  
Needs["GraphUtilities`"]  

n=300;  
pts=LineScaledCoordinate[points,N@(#/n)]&/@Range[0,n];

However with this code were not included in the list points. Then with the function below I've added.

pts=Insert[pts,points[[2]],107];  
pts=Insert[pts,points[[3]],177];

I added these points in the correct position because I searched by hand and applied the function.
This is the first question:
How do you find these positions in an automatic way?

With that done, with these new items i created divisions where these points are at the end of each list.
How could I do that these points are reference for these divisions?

list1=pts[[#,1]]&/@Range[107];  
list2=pts[[#,1]]&/@Range[108,177];  
list3=pts[[#,1]]&/@Range[178,303];

kglr · Answer 1 · 2016-10-11T19:09:58.123

3

Nearest[pts ->Automatic] /@ points (*thanks: MichaelE2 *)

{{1}, {107}, {177}, {301}}

pointsandpos = Thread[{points[[2 ;; -2]], {0, 1} + 
    Flatten[Nearest[pts -> Automatic] /@ points[[2 ;; -2]]]}];

newpts = Fold[Insert[#, ## & @@ #2] &, pts, pointsandpos];

ListPlot[{points, newpts}, Joined -> { False, True}]

Mathematica graphics

edited Oct 11 '16 at 19:09

answered Oct 11 '16 at 18:23

kglr

394,356
18
477
896

Nearest[pts -> Automatic] is more efficient. – Michael E2 Oct 11 '16 at 18:27
It's unclear, I guess, whether the index returned is before or after the vertex. – Michael E2 Oct 11 '16 at 18:28
@kglr I made a test with your answer and appears duplicate points – LCarvalho Oct 12 '16 at 11:23
@kglr Test: Position[newpts, 5] and Position[newpts, 10] – LCarvalho Oct 12 '16 at 11:25
What I meant about the index is that in the OP's example the two interior indices returned by Nearest, {107}, {177}, are points that come just after the nearest vertex (points[[2]], points[[3] resp.). In another configuration, they might come before depending on the nearest point to the vertex. Then the offsets you add, {0, 1}, to get pointsandpos would have to be changed. I doubt that even Nearest[..][p, 2] would bracket the point p. Think of a tall narrow "W." – Michael E2 Oct 23 '16 at 01:53

Michael E2 · Answer 2 · 2016-10-14T12:42:03.283

The "positions" of the corners can be found as follows;

distances = Accumulate[EuclideanDistance @@@ Partition[points, 2, 1]];
pos = 1 + n*Most[distances]/Last[distances]
(*  {106.556, 176.556}  *)

The fractional part can be interpreted as a interpolation between the points with positions {{106}, {107}} and {{176}, {177}} respectively. The vertices can be inserted, therefore, between them.

To split the list pts, maybe this?

lists = {list1, list2, list3} = 
  pts[[#]] & /@ 
   Rest@FoldList[Span[#[[-1]] + 1, #2] &, {0}, Append[Floor[pos], n + 1]];

gpts = Thread@{{Red, Green, Blue}, Point /@ lists}; (* graphics for pts *)
Graphics[{
  gpts,
  Black, PointSize@Medium, Point[points[[2 ;; 3]]]}]

Mathematica graphics

For just the first coordinate, change pts[[#]] to pts[[#, 1]].

Alternatively, you can use LineScaledCoordinate to get the equally spaced points together with points, in case that is desired:

pts2 = LineScaledCoordinate[points, #] & /@ 
  Union[Range[0., 300]/n, Most[distances]/Last[distances]];

Position[pts2, p_ /; AnyTrue[points, p == # &]]
(*  {{1}, {107}, {178}, {303}}  *)

Update: If you want the 2nd and 3rd points appended to the ends of the first two segments...

First note I added lists = {list1, list2, list3} to the original answer above. It's not clear to me whether a list of lists or the separate lists is a better data structure for the actual use case, so I'll show both simulatneously.

Next note that the code correctly splits pts at points:

GraphicsRow[
 Graphics[{Line[points], PointSize[Large], gpts},
    PlotRange -> Outer[Plus, #, {-0.2, 0.2}]] & /@ points[[2 ;; 3]]
 ]

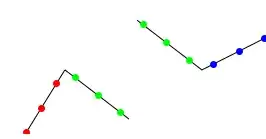
Mathematica graphics

The easiest way to append a couple of points is to Append them.

(* append points[[2]], points[[3]] and update the lists *)
lists[[1 ;; 2]] = {list1, list2} =
   MapThread[Append, {Most@lists, points[[2 ;; 3]]}];
gpts = Thread@{{Red, Green, Blue}, Point /@ lists};   (* update graphics *)
GraphicsRow[
 Graphics[{Line[points], PointSize[Large], gpts},
    PlotRange -> Outer[Plus, #, {-0.2, 0.2}]] & /@ points[[2 ;; 3]]
 ]

Mathematica graphics

Now the OP doesn't show this, but one might want to prepend the endpoint(s) of the (middle) segment(s) as well. For that there's Prepend[]....

@LMC I don't think Ceiling[pos] is right: it gives http://i.stack.imgur.com/4JUmV.png -- Please explain further what's wrong with Floor[pos]; otherwise, Floor seems correct and I will roll back. — Michael E2, Oct 13 '16 at 21:07
@LMC I appreciate your intention, but please test your "fixes" first. So far, none of them has done what you want. The last one produces an error. — Michael E2, Oct 14 '16 at 12:43

score 2 · Accepted Answer · edited Apr 13 '17 at 12:55

This is a answer based on the solution of Michael E2.

I would like to offer my attempts without damaging the response that does not belong to me.

My attempts

Here is the list pts without the values from the list points

Clear["Global`*"]
points = {{0, 0}, {5, 8.07774721}, {10, 4.24499363}, {20, 9.28880172}};
Needs["GraphUtilities`"]

n = 300;
pts = LineScaledCoordinate[points, N@(#/n)] & /@ Range[0, n];

With the function below it is possible to structure the points from the list points in pairs with offset value 1.

Partition[points, 2, 1]

$\left( \begin{array}{cc} \{0,0\} & \{5,8.07775\} \\ \{5,8.07775\} & \{10,4.24499\} \\ \{10,4.24499\} & \{20,9.2888\} \\ \end{array} \right)$

With the function below it is possible to get the lengths between the pairs mentioned above

partialPath = EuclideanDistance @@@ Partition[points, 2, 1] // N

$\{9.5,6.3,11.2\}$

With the function below it is possible to make the accumulated form sum

Accumulate[partialPath]

$\{9.5,15.8,27.\}$

With the function below it is possible to delete the last element of the accumulated numbers list

Most@Accumulate[partialPath]

$\{9.5,15.8\}$

With the function below it is possible to use the last element of the accumulated numbers list

Last@Accumulate[partialPath]

$27$

With the function below it is possible to get the percentage of each path with the full path

porcentPath = {#/Last@Accumulate[partialPath]} & /@Most@Accumulate[partialPath]

$\left( \begin{array}{c} 0.351852 \\ 0.585185 \\ \end{array} \right)$

With the function below, it is possible to separate the points in the points list that are not included in the pts list

valuesPositions = Rest@Most@points

$\left( \begin{array}{cc} 5 & 8.07775 \\ 10 & 4.24499 \\ \end{array} \right)$

With the function below it is possible to identify which positions in should be inserted the values {5,8.07774721} and {10,4.24499363}

pos = Flatten@Transpose[Ceiling[n*porcentPath] + 1]

$\{107,177\}$

With the function below it is possible to define a list to be added values, the values to be added and the positions they should be inserted.

InsertValuePosition[list_, values_, positions_] := 
 Fold[Insert[#, #2[[1]], #2[[2]]] &, list, Transpose[{values, positions}]]
pts = InsertValuePosition[pts, valuesPositions, Transpose[{pos}]]

With the function below it is possible to subdivide the pts list in three other lists where the entered values are at the end of the two first lists

FoldPairList[TakeDrop, pts, Flatten@{0, pos, Length@pts} // Differences]

Adding points limits

3 Answers3

Linked