1

I'm trying get the critical points of the function $f(x)=(( 1 - 3*(x + 1)^3)/(x^4 + 1))*(x - 2)$ so I took the derivative which is $(16 + 18 x - 9 x^2 - 28 x^3 - 48 x^4 - 18 x^5 + 3 x^6)/(1 + x^4)^2$ and typed:

Roots[16 + 18 x - 9 x^2 - 28 x^3 - 48 x^4 - 18 x^5 + 3 x^6 == 0, x]

And it gives me this six times, only changing the number after &,:

 x == Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 1]

I'm new to this program so I was expecting an actual number. What does that mean and how can I get the critical point or get a number for the root ?

jerry232
  • 11
  • 1
  • Check out the Root documentation: http://reference.wolfram.com/language/ref/Root.html – ktm Oct 12 '16 at 16:55
  • 1
    See this. – J. M.'s missing motivation Oct 12 '16 at 16:56
  • Welcome! I suggest the following:
    1. As you receive help, try to give it too, by answering questions in your area of expertise.
    2. Take the tour and check the faqs!
    3. When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign!
     –  Oct 12 '16 at 16:58
  • 1
    Sixth order polynomials don't have a general closed-form solution except for some special cases - Roots represents these roots for potential further processing. If you want numerical approximations, you can either 1) wrap the Roots command in N, or 2) use NSolve to get "actual numbers". – corey979 Oct 12 '16 at 17:12

2 Answers2

1
f[x_] := ((1 - 3*(x + 1)^3)/(x^4 + 1))*(x - 2)

Plot[{f[x], f'[x]}, {x, -7, 7}, Frame -> True, PlotLegends -> "Expressions"]

enter image description here

roots1 = x /. Solve[f[x] == 0, x]

$\left\{2,\frac{1}{\sqrt[3]{3}}-1,-1-\frac{1-i \sqrt{3}}{2 > \sqrt[3]{3}},-1-\frac{1+i \sqrt{3}}{2 \sqrt[3]{3}}\right\}$

ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ roots1, AspectRatio -> 1, PlotStyle -> Red]

enter image description here

Plot[f[x], {x, -5, 5}, Epilog -> {Red, PointSize[Large], Point[{{roots1[[1]], 
0}, {roots1[[2]], 0}}]}]

enter image description here

roots2 = x /. Solve[f'[x] == 0, x]

{Root[16+18 #1-9 #1^2-28 #1^3-48 #1^4-18 #1^5+3 #1^6&,1],Root[16+18 #1-9 #1^2-28 >#1^3-48 #1^4-18 #1^5+3 #1^6&,2],Root[16+18 #1-9 #1^2-28 #1^3-48 #1^4-18 #1^5+3 >#1^6&,3],Root[16+18 #1-9 #1^2-28 #1^3-48 #1^4-18 #1^5+3 #1^6&,4],Root[16+18 #1-9 >#1^2-28 #1^3-48 #1^4-18 #1^5+3 #1^6&,5],Root[16+18 #1-9 #1^2-28 #1^3-48 #1^4-18 >#1^5+3 #1^6&,6]}

ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ roots2, AspectRatio -> 1, PlotStyle -> Red]

enter image description here

N[roots2]

{-1.57785,-0.714464,0.703213,8.11693,-0.263913-0.871319 I,-0.263913+0.871319 I}

NSolve[{f[x] == 0}, x]

{{x->2.},{x->-1.34668+0.600468 I},{x->-1.34668-0.600468 I},{x->-0.306639}}

NSolve[{f[x] == f'[x]}, x, Reals]

{{x -> 2.60019}, {x -> -1.35042}, {x -> -0.840415}, {x -> 0.51624}}

1
Clear[f]

f[x_] = (1 - 3*(x + 1)^3)/(x^4 + 1)*(x - 2);

roots = x /. Solve[f[x] == 0, x]

(*  {2, -1 + 1/3^(1/3), -1 - (1 - I Sqrt[3])/(2 3^(1/3)), -1 - (1 + I Sqrt[3])/(
  2 3^(1/3))}  *)

The radicals can be expressed as Root objects

roots // RootReduce

(*  {2, Root[2 + 9 #1 + 9 #1^2 + 3 #1^3 &, 1], 
 Root[2 + 9 #1 + 9 #1^2 + 3 #1^3 &, 3], Root[2 + 9 #1 + 9 #1^2 + 3 #1^3 &, 2]}  *)

And low-order Root objects can be expressed by radicals using ToRadicals

% // ToRadicals

(*  {2, -1 + 1/3^(1/3), -1 - (1 - I Sqrt[3])/(2 3^(1/3)), -1 - (1 + I Sqrt[3])/(
  2 3^(1/3))}  *)

% === roots

(*  True  *)

Either radicals or Root objects can be converted to approximate numeric values by N

roots // N

(*  {2., -0.306639, -1.34668 + 0.600468 I, -1.34668 - 0.600468 I}  *)

critPts = x /. Solve[f'[x] == 0, x]

(*  {Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 1], 
 Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 2], 
 Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 3], 
 Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 4], 
 Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 5], 
 Root[16 + 18 #1 - 9 #1^2 - 28 #1^3 - 48 #1^4 - 18 #1^5 + 3 #1^6 &, 6]}  *)

The order of these polynomials are too high to express as radicals but can be expressed as approximate numeric values with N

critPts // N

(*  {-1.57785, -0.714464, 0.703213, 8.11693, -0.263913 - 0.871319 I, -0.263913 + 
  0.871319 I}  *)

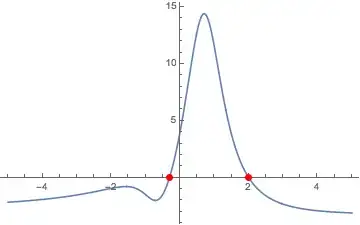
Plot[f[x], {x, -3, 10}, PlotRange -> All,
 Epilog -> {AbsolutePointSize[6], Red,
   Point[{#, f[#]} & /@
     Cases[critPts, _?(Im[#] == 0 &)]],
   Blue, Point[{#, f[#]} & /@
     Cases[roots, _?(Im[#] == 0 &)]]},
 PlotLegends -> PointLegend[{Red, Blue},
   {"Critical Point", "Root"}]]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198