Arc length of a 3D set of points

Question

Suppose I have a data set of 3D coordinates that form a pretty continuous path in space. I would like to measure the total arc length (or path length) of the entire system. At this point the coordinates are not connected.

Answer 1

The very best method

Bob Hanlon, in a comment below, solved the issue with what I further call an "ingenious method":

Total[RegionMeasure@*Line /@ (list[[#]] & /@ FindCurvePath[list])]

working with list of points forming a nicely behaving (e.g., no loops) curve in 2D or 3D.

---

Straightforward approach

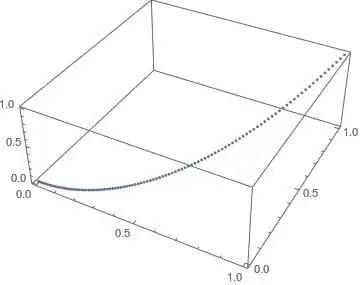
data = Table[{x, x^2, x^3}, {x, 0, 1, 0.01}];

ListPointPlot3D @ data

The "exact" result in this case is

NIntegrate[Norm @ D[{x, x^2, x^3}, x], {x, 0, 1}]

1.86302

A rough estimate might be the sum of distances between consecutive pairs of points:

Total @ (EuclideanDistance @@@ Partition[data, 2, 1])

1.86301

or in a compact form

RegionMeasure @ Line[data] (* thanks: Szabolcs *)

1.86301

or

ArcLength @ Line @ data (* thanks: JasonB *)

1.86301

---

Overcoming some caveats

The above assumes that the points are ordered in the "correct" way. Simple Sort won't work when the curve "runs back", and the points are not in the correct order. As an illustration let's take

f[x_] := -1 + 4 x - 4 x^2 + x^3

data2 = Table[{f[x], x^2, x^3}, {x, 0, 3, 0.01}];

ListPointPlot3D @ data2

NIntegrate[Norm @ D[{f[x], x^2, x^3}, x], {x, 0, 3}]

30.0472

and

RegionMeasure @ Line[data2]

30.0472

or

ArcLength @ Line @ data2

30.0472

coincide nicely. Here's what happens when the points are in random order:

data3 = RandomSample @ data2;

RegionMeasure @ Line[data3]

2747.76

and Sort fails miserably:

RegionMeasure @ Line[Sort@data3]

1548.66

I define a set

data4 = data3;

in which I find the "smallest" point:

start = Min /@ Transpose@data4

{-1., 0., 0.}

which for future use I'll make a copy of:

s0 = {start};

and now I seek point after point the point nearest to the preceding:

data5 = s0~Join~Reap[Do[
      data4 = Complement[data4, {start}]; 
      Sow[start = Nearest[data4, start][[1]]];, {i, 300}
      ]
     ][[2, 1]];
(* I guess this could be done in a different way, possibly with NestList, or with some other ingenious method *)

which gives

data5 == data2

True

and of course

RegionMeasure @ Line[data5]

30.0472

---

Another approach can employ FindShortestTour (thanks: JulienKluge and Rahul):

start = Min /@ Transpose@data3
end = Max /@ Transpose@data3

t1 = Max @ Position[data3, start]
t2 = Max @ Position[data3, end]

First @ FindShortestTour[data3, t1, t2]

30.0472

---

Wrapping things up in a single function

curveLength[data_] := Block[{data4 = data, start, s0, data5},
  start = Min /@ Transpose@data4;
  s0 = {start};
  data5 = s0~Join~Reap[Do[
       data4 = Complement[data4, {start}]; 
       Sow[start = Nearest[data4, start][[1]]];, {i, 
        Length @ data4 - 1}
       ]
      ][[2, 1]];
  RegionMeasure @ Line[data5]
  ]

curveLength[data]

1.86301

---

ISSUE

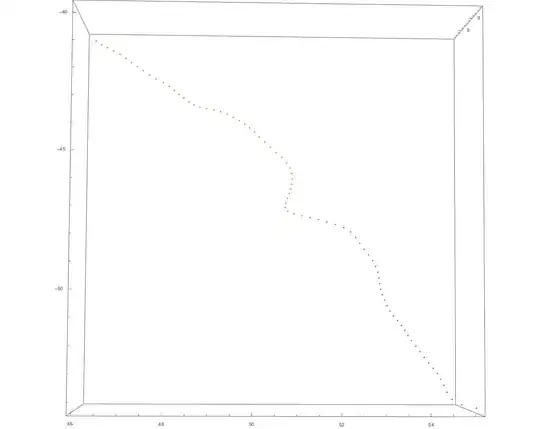
None of the above approaches (except for the FindCurvePath one) will work with curves like this:

because the starting point was found as a point with its coordinates smallest in the data set, which is not the case now. One can of course provide the starting point manually, and then the length of the curve can be still obtained.