How to plot a function?

Question

Let's assume a box-function and a convolution:

f = UnitBox[x];
c[t_] := Convolve[t, t, x, y] /. y -> x;
c[f]

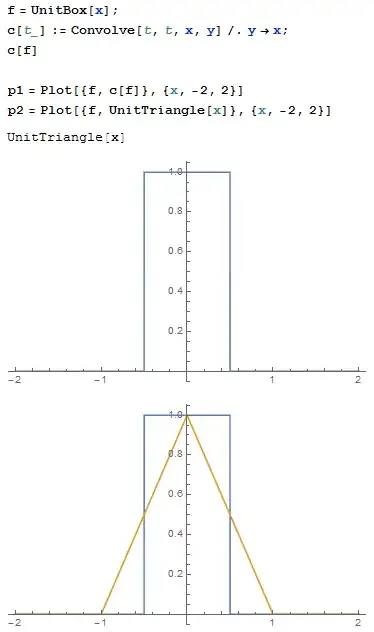
My problem arises when plotting the functions. Why does the code p2 work and the code p1 not? Where is the difference?

p1 = Plot[{f, c[f]}, {x, -2, 2}]
p2 = Plot[{f, UnitTriangle[x]}, {x, -2, 2}]

p1 = Plot[{f, Evaluate@c[f]}, {x, -2, 2}] – Sumit Oct 13 '16 at 09:07 — Sumit, Oct 13 '16 at 09:07

score 4 · Answer 1 · answered Oct 13 '16 at 09:09

4

f = UnitBox[x];
c[t_] := Convolve[t, t, x, y] /. y -> x;
p1 = Plot[{f, Evaluate@c[f]}, {x, -2, 2}]
p2 = Plot[{f, UnitTriangle[x]}, {x, -2, 2}]

answered Oct 13 '16 at 09:09

Sumit

15,912
2
31
73

score 3 · Answer 2 · edited Apr 13 '17 at 12:55

Just for fun (as Sumit has answered question). Also search site for questions and posts such as this.

f = UnitBox[x];
c[t_] := Convolve[t, t, x, y] /. y -> x;
c[f];
cn[t_] := Integrate[f UnitBox[t - x], {x, -Infinity, Infinity}];

Animate[Plot[{f, c[f], UnitBox[x - p]}, {x, -2, 2},
  Filling -> {3 -> {Axis, LightRed}, 1 -> {3}},
  Evaluated -> True,
  Epilog -> {Red, PointSize[0.02], Point[{p, cn[p]}]},
  Exclusions -> None], {p, -2, 2}]

How to plot a function?

2 Answers2