How do I plot the solutions of
Sum[cf1[[i, 2]] E^(-r cf1[[i, 1]]), {i, Length@cf1}] == 0
where
cf1 = {{0, -100}, {1, 10}, {2, 10}, {3, 110}}
as lines on the complex plane?
The equation is an simple example of an internal rate of return problem.
To restate, I know that FindRoot will give me the answer in reals. I want to demonstrate that, on the complex plane, the answer is much more, ahh..., complex.
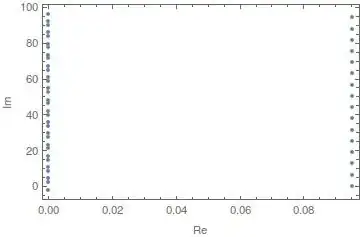
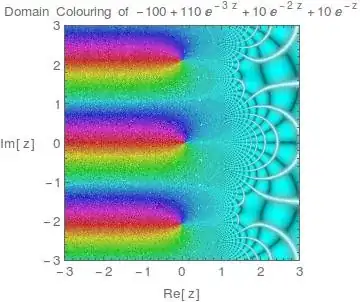

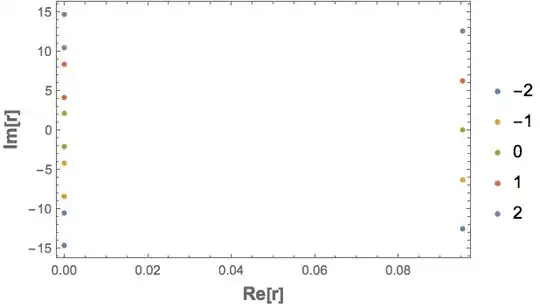
rsupposed to be? – J. M.'s missing motivation Oct 13 '16 at 13:38