How to avoid Root[] when using Solve[]

Question

I am trying to solve a system of algebraic equations using Solve. The solution Mathematica gives use Root[] as an intermediate:

m5 = {{k - m w^2, -k, 0, 0, 0}, {-k, 2 k - m w^2, -k, 0, 0}, {0, -k, 2 k - m w^2, -k, 0}, {0, 0, -k, 2 k - m w^2, -k}, {0, 0, 0, -k, k - m w^2}};

sol = Solve[Det[m5] == 0 , w, Reals]

The output looks like

{{w -> ConditionalExpression[0, (k > 0 && m > 0) || (k > 0 && m < 0) || (k < 0 && m > 0) || (k < 0 && m < 0)]}, 
 {w -> ConditionalExpression[Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 1], (k > 0 && m > 0) || (k < 0 && m < 0)]}, {w -> ConditionalExpression[ Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 2], (k > 0 && m > 0) || (k < 0 && m < 0)]}, 
 {w -> ConditionalExpression[Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 3], (k > 0 && m > 0) || (k < 0 && m < 0)]}, 
 {w -> ConditionalExpression[Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 4], (k > 0 && m > 0) || (k < 0 && m < 0)]},
 {w -> ConditionalExpression[Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 1], (k > 0 && m > 0) || (k < 0 && m < 0)]},
 {w -> ConditionalExpression[Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 2], (k > 0 && m > 0) || (k < 0 && m < 0)]},
 {w -> ConditionalExpression[Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 3], (k > 0 && m > 0) || (k < 0 && m < 0)]},
 {w -> ConditionalExpression[Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 4], (k > 0 && m > 0) || (k < 0 && m < 0)]}}

Even if I use Simplify[] to state the assumptions

sol = Simplify[sol, Assumptions -> {k > 0, m > 0}]

I still cannot get rid of Root[] in the solution

{{w -> 0}, {w -> Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 1]},
 {w -> Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 2]},
 {w -> Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 3]}, 
 {w -> Root[5 k^2 - 5 k m #1^2 + m^2 #1^4 &, 4]}, 
 {w -> Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 1]}, 
 {w -> Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 2]}, 
 {w -> Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 3]}, 
 {w -> Root[k^2 - 3 k m #1^2 + m^2 #1^4 &, 4]}}

This is annoying because the quartics are well solvable. Can anyone help please?

Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — Michael E2, Oct 14 '16 at 01:24

score 4 · Accepted Answer · answered Oct 14 '16 at 00:57

4

From the documentation of ToRadicals:

ToRadicals[expr] attempts to express all Root objects in expr in terms of radicals.

Hence simply

sol = Solve[Det[m5] == 0 , w, Reals]
ToRadicals @ sol

Moreover, you can get rid of the ConditionalExpressions with Normal, which in this case assumes that all the conditions are met and only displays the formulae:

answered Oct 14 '16 at 00:57

corey979

23,947
7
58
101

3

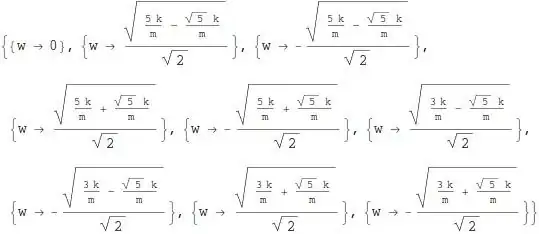
The OP was fortunate here that the expressions of interest were expressible in radicals. This is of course not the case in general. – J. M.'s missing motivation Oct 14 '16 at 03:35
I like this solution best. Intuitive and straightforward. Thanks. – Dan Zhang Oct 14 '16 at 21:14

score 3 · Answer 2 · answered Oct 14 '16 at 00:57

Does this work for you? You can try 5th order. Mathematica finds solution. Replace w^2 by z

ClearAll[k, m, w, s, s]
m5 = {{k - m w^2, -k, 0, 0, 0}, {-k, 2 k - m w^2, -k, 0, 0}, {0, -k, 
    2 k - m w^2, -k, 0}, {0, 0, -k, 2 k - m w^2, -k}, {0, 0, 0, -k, 
    k - m w^2}};
d = Det[m5]

Mathematica graphics

d = d /. w -> z^(1/2)

Mathematica graphics

s = Solve[d == 0, z]

Mathematica graphics

Now replace back and solve for w

s = Flatten[(s /. z -> w^2) /. Rule -> Equal]

Mathematica graphics

Solve[#, w] & /@ s

Mathematica graphics

How to avoid Root[] when using Solve[]

2 Answers2