In a meteorology textbook (Hogan & Mason, 2012) the following system is specified:
n isn't specified above, but it's just a+b+c+d.
I tried to use Mathematica to reproduce the results from this textbook, in which a b c d are replaced with H F s. The following code works out PC in a few seconds:
eqn = {p == (a + d)/(a + b + c + d), s == (a + c)/(a + b + c + d),
h == (a)/(a + c), f == b/(b + d)}
Solve[eqn, {p}, {a, b, c, d}]
Then I tried to work out DSS:
eqn = {p == (ad - bc)/(Sqrt[(a + b) (c + d) (a + c) (b + d)]),
s == (a + c)/(a + b + c + d), h == (a)/(a + c), f == b/(b + d)}
Solve[eqn, {p}, {a, b, c, d}]
Mathematica ran for hours and couldn't work out the solution.
Googling I found a forum thread that suggested to improve speed by putting assumptions on the variables. I can assume that a b c d are non-negative integers and that n is a positive integer and that p h f s are non-negative reals. I can further assume that h f s are >= 0 and <= 1, and that p is >= -1 and <= 1.
The documentation for Solve doesn't indicate any way to put assumptions on the variables. I tried the simple solution
Solve[eqn, {p}, {a, b, c, d}, Reals]
but that also just kept running for ages.
Then I tried adapting @MarcoB's solution from this thread, I tried:
Assuming[
{{p, f, h, s} \[Element] Reals, {a, b, c, d} \[Element] Integers,
p >= -1, p <= 1, f >= 0, f <= 1, h >= 0, h <= 1, s >= 0, s <= 1},
Simplify[
Solve[eqn, {p}, {a, b, c, d}]
]
]
This also ran for hours without reaching a solution. Can anyone explain why Mathematica is not reaching a solution? I get that the DSS system is more complicated than the PC system, but it surprised me that this difference was sufficiently large that it precluded Mathematica from reaching an answer.
Hogan, R. J., & Mason, I. B. (2012). Deterministic forecasts of binary events. Forecast Verification: A Practitioner's Guide in Atmospheric Science, Second Edition, 31-59. Chicago.
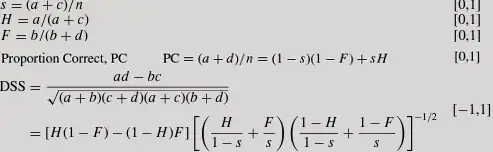
adis a single variable;a dis the same asa*d; which do you want? Adding theSqrtdoubles the underlying degree of the system, not to mention all the extra products, which makes it considerably harder to solve. – Michael E2 Oct 14 '16 at 02:15(a d - b c)– user1205901 - Слава Україні Oct 14 '16 at 06:37