For example I can construct:
row1 = D[f(x,y),x,#]&/@{x,y}
row2 = D[f(x,y),x,#]&/@{x,y}
then:
matrix = {row1,row2}
That yields a matrix like:
$$\left(\matrix{\frac{\partial^2 f}{\partial x^2} \quad\frac{\partial^2 f}{\partial x\partial y}\\ \frac{\partial^2 f}{\partial y\partial x}\quad \frac{\partial^2f}{\partial y^2}}\right)$$
Question: how to construct such matrix in a single line of code?
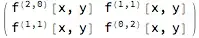
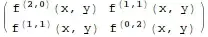
Outer[Dt[f, #1, #2] &, #, #] &@{x, y}– wxffles Oct 16 '16 at 20:18D[f[x, y], {{x, y}, 2}]. – b.gates.you.know.what Oct 16 '16 at 20:29