Instead of the Del symbol (which has no built-in meaning) you need the gradient operator. What you're looking for can be achieved by using Map to apply the dot product of $\vec{u}$ and Grad to each row of the vector. I define this as the convective derivative dConvect and apply it to a test vector uVec:
uVec = Through[{Subscript[u, \[ScriptX]], Subscript[u, \[ScriptY]],
Subscript[u, \[ScriptZ]]}[x, y, z, t]];
dConvect[vec_] := D[vec, t] + ((vec.Grad[#, {x, y, z}]) & /@ vec)
dConvect[uVec] // MatrixForm // TraditionalForm
The output is a little ugly, so I'll add some better formatting before displaying the result:
Derivative /:MakeBoxes[Derivative[\[Alpha]__][f1_][vars__?AtomQ],
TraditionalForm] :=
Module[{bb, dd, sp},
MakeBoxes[dd, _] ^=
If[Length[{\[Alpha]}] == 1, "\[DifferentialD]", "\[PartialD]"];
MakeBoxes[sp, _] ^= "\[ThinSpace]";
bb /: MakeBoxes[bb[x__], _] := RowBox[Map[ToBoxes[#] &, {x}]];
TemplateBox[{ToBoxes[bb[dd^Plus[\[Alpha]], f1]],
ToBoxes[Apply[bb,
Riffle[Map[
bb[dd, #] &, (Pick[{vars}, #]^Pick[{\[Alpha]}, #] &[
Thread[{\[Alpha]} > 0]])], sp]]],
ToBoxes[Derivative[\[Alpha]][f1][vars]]}, "ShortFraction",
DisplayFunction :> (FractionBox[#1, #2] &),
InterpretationFunction :> (#3 &), Tooltip -> Automatic]]
Format[Subscript[u, s_][x, y, z, t]] := Subscript[u, s];
dConvect[uVec] // MatrixForm // TraditionalForm
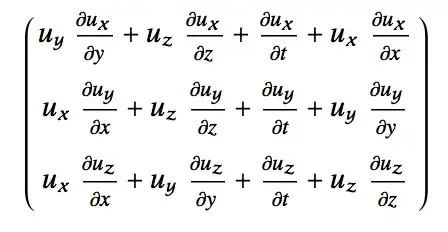
The formatting uses this answer.
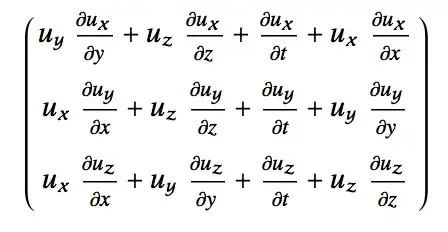
dConvectwon't find all the terms if I try it in Spherical Coordinates. I wonder how you'd do this? – Matt Rogers Feb 03 '21 at 17:56