11

Bug introduced in 10, fixed in 11.1.

I want to solve the electromagnetic wave equation in frequency domain. A known solution, a plane wave Exp[ I k0 x] is used to set the Dirichlet conditions to all the boundaries. I expect to get the plane wave solution. The following code runs well ,but the result is strange. I don't know why. It seems high-frequency oscillation occurs. Is there some options to eliminate the unusual oscillation? thanks a lot! 

<< NDSolve`FEM`  

λ = 0.53; k0 = 2 π/λ; R = λ;

mesh = ToElementMesh[FullRegion[2], {{0, R}, {0, R}}, 
   "MaxCellMeasure" -> 0.0005];

mesh["Wireframe"]

op = 
  Most[Curl[Curl[{u[x, y], v[x, y], 0}, {x, y, z}], {x, y, z}] - 
   k0^2 {u[x, y], v[x, y], 0}]

pde = op == {0, 0};

Subscript[Γ, D] = 
  DirichletCondition[{u[x, y] == 0., v[x, y] == Exp[I k0 x]}, True];

{us, vs} = 
  NDSolveValue[{pde, Subscript[Γ, D]}, {u, v}, {x, y} ∈ mesh]

DensityPlot[Re[vs[x, y]], {x, y} ∈ mesh, 
  ColorFunction -> "Rainbow", 
  PlotLegends -> Automatic, 
  PlotPoints -> 50, 
  PlotRange -> All]

enter image description here

user21
  • 39,710
  • 8
  • 110
  • 167
quantum
  • 111
  • 3
  • 3
    What's your question? – Feyre Oct 23 '16 at 16:08
  • 4
    I'm voting to close this question as off-topic because the code posted does not produce any errors when evaluated. There does not seem to be any question to answer. – m_goldberg Oct 23 '16 at 16:37
  • The question is probably: "Why does this output not agree with the known analytical solution $v(x,y) = e^{ik_0x}$ and $u(x,y) = 0$?" – Michael Seifert Oct 24 '16 at 16:34
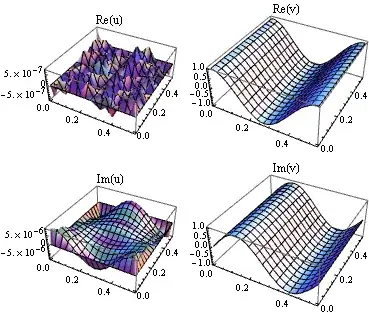
  • I don't have a complete solution yet, but here are my thoughts: (1) the "high-frequency" oscillation is at the "frequency" of the mesh you're using. Reducing MaxCellMeasure alleviates this. (2) Solving the equation $\nabla^2 v = -k_0^2 v$ (which should be equivalent to the above equations as long as $\partial u/\partial x + \partial v/\partial y = 0$) yields a well-behaved result. If I have time, I'll come back to this later. – Michael Seifert Oct 24 '16 at 17:04
  • 1
    Thank you, I have made a mistake. For a electromagnetic wave , Div(E)==0 should satisfied. To solve Helmholtz equation is the correct choice. – quantum Oct 24 '16 at 23:25
  • My first attempt is to simulate the propagation of electromagnetic wave in different media and seems got the answer by solve Laplacian[Bz]+k0^2*Bz==0,then got electric field by grad(Bz), but with low precision. So I try to solve the electric field directly but don't know how to add Div(E)==0 to the equations. I tried another method but got the complain of "nonlinear coefficient unsupported" , so low-level progamming may be unavoidable. – quantum Oct 25 '16 at 00:01
  • 1
    It seems to work if you replace Exp[I k0 x] by Cos[k0 x] in the DirickletCondition[...] ?? – andre314 Oct 28 '16 at 20:28
  • @andre Interesting, seems that trouble is made by the imaginary part of the boundary. Maybe you can make this into an answer? – xzczd Nov 01 '16 at 10:22
  • @xzczd I don't dare to do an answer because my ideas are not enough clear about this (on the theorical point of view). Feel free do it (or someone else). – andre314 Nov 01 '16 at 18:41
  • As I understand it, the code works well in 13.0.0. – user64494 Feb 08 '22 at 16:29

1 Answers1

9

Update

OP's code produces the correct result since v11.1, I think it's safe to say the "noisy" result is caused by a bug.

Here's a solution based on finite difference method (FDM). The definition of pdetoae (a general purpose function discretizing PDE to algebraic equations with finite difference formula) can be found here. 

λ = 53/100; k0 = 2 π/λ; R = λ;

op = Most[Curl[Curl[{u[x, y], v[x, y], 0}, {x, y, z}], {x, y, z}] - 
    k0^2 {u[x, y], v[x, y], 0}];

pde = op == {0, 0};
bc = Function[{x, y}, {u[x, y] == 0, v[x, y] == Exp[I k0 x]}] @@@ {{0, y}, {R, y}, {x, 
      0}, {x, R}} // Flatten;

domain = {0, R};
points = 50;
grid = Array[# &, points, domain];
difforder = 4;
(*Definition of pdetoae isn't included in this code piece,
  please find it in the link above. *)
ptoa = pdetoae[{u, v}[x, y], {grid, grid}, difforder];
del = Most@Rest@# &;

ae = del /@ del@# & /@ ptoa@pde;
aebc = MapAt[del, ptoa@bc, List /@ Range@4];
{b, mat} = CoefficientArrays[{ae, aebc} // Flatten, 
   Outer[#[#2, #3] &, {u, v}, grid, grid] // Flatten];
sollst = LinearSolve[-mat, N@b];
solmat = ArrayReshape[sollst, {2, points, points}];
{solu, solv} = ListInterpolation[#, {grid, grid}] & /@ solmat;

Outer[Plot3D[#@First[#2][x, y], {x, 0, R}, {y, 0, R}, PlotLabel -> #@Last@#2] &, {Re, 
   Im}, {{solu, "u"}, {solv, "v"}}, 1] // Grid

Mathematica graphics

Remark

  1. Number of grid points i.e. points should be even, or the error of $\text{Im}(v)$ will be quite large, I'm not sure about the reason.

  2. Difference order i.e. difforder should be even and greater than 2, or the error will be large and seems unlikely to be alleviated by increasing points. I guess this might explain why OP's code doesn't work well, because according to this document page, the default "MeshOrder" of ToElementMesh is exactly 2, but since I'm still in v9 and the Wolfram Cloud is too slow, I'd like to stop here.

xzczd
  • 65,995
  • 9
  • 163
  • 468
  • Thank you! you code has help me to understand the EM wave equations better. Considering the ability to handle arbitrarily shaped regions I will continue to study FEM. – quantum Oct 25 '16 at 14:12