How can I find the surface area of an image in mathematica?

Question

Would I binarize the image and then find the area of the irregular shape?

Answer 1

I take it, that you need to measure the area of an irregular plate in the senter of the image. If so, I have a solution.

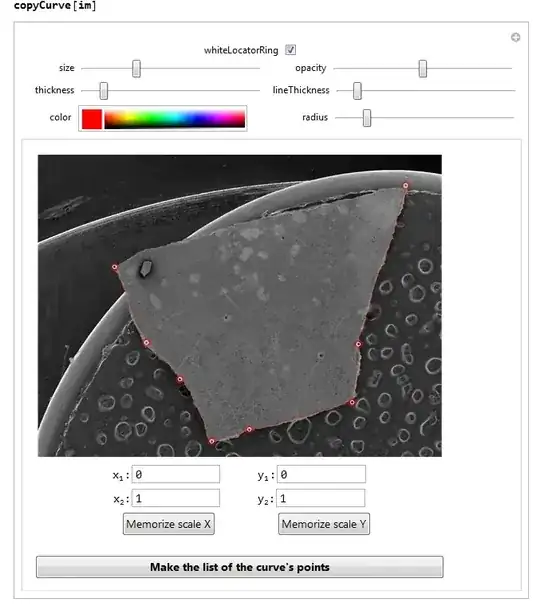
Some time ago I published here a function copyCurve. You can find this function along with a detailed description here. The argument of this function can be any image. So you need to copy your image and insert it into Mma wrapped by Image. Like this:

Then apply the copyCurvefunction:

The use of the function is described here, have a look. Since you did not give the dimensions of the image, I assumed them to be 1 in the both directions. It, thus, spans from x1=0 to x2=1 and from y1=0 to y2=1, as you see below the image in the text fields of the manipulator. You will enter your correct dimensions, as it is described in my post.

With this function you need to define points of the boundary of your object by inserting locators (Alt+LeftClick). The locators have a form of red circles in the image below.

!!

For our purpose it is important that you only take points with the increasing coordinate X. So, you start from the utmost left corner of the part of the boundary that you are taking now.

!!

You then press the button, and evaluate the variable listOfPoints in a separate cell. It returns a list of points, which you copy-paste into another cell and give it the name lst1. In my case it had this value:

lst1 = {{0.188`, 0.629`}, {0.265`, 0.369`}, {0.367`, 0.243`}, {0.426`,
 0.05`}, {0.52`, 0.088`}, {0.781`, 0.2`}, {0.794`, 
0.385`}, {0.878`, 0.735`}, {0.917`, 0.892`}};

For the same reason we have to collect the points from the top and from the bottom parts separately, again starting from the utmost left point: Here is the bottom part:

you get analogously the list lst2. In my case it is

lst2 = {{0.188`, 0.629`}, {0.261`, 0.686`}, {0.372`, 0.718`}, {0.56`, 
0.786`}, {0.726`, 0.842`}, {0.851`, 0.886`}, {0.917`, 0.892`}};

Now we can form a common list and with its use draw a polygon:

    lst = Join[{lst1, lst2}] // Flatten[#, 1] &;
Graphics[{Red, Polygon[lst]}]

It is important to draw in order to make sure that we, indeed, obtained a polygon. It will not be the case if the order of the points will be different.

Now we can calculate the area of the polygon:

Polygon[lst] // Area

(* 0.334798 *)

Done, have fun!

Answer 2

Okay, this is not a really good answer, partly because it was derived by trial and error. I hope someone else gives a better one so i could also learn from it.

However, here is the code i used:

ri=Dilation[Opening[DeleteSmallComponents[Colorize@MorphologicalComponents[ImageAdjust[DistanceTransform[Blur[img,2],0.25]],0.05]],40],DiskMatrix[20]];
ImageCompose[img,{ri,0.5}]

I found it particulary hard to let the code ignore the "thing" (top, left) and to distinguish between the plate and the edge of the disk it lays on.

But in the end, i think the measurement is pretty decent. Assuming for example your image is $100\mu m\times50 \mu m$ we can calc:

(ComponentMeasurements[MorphologicalComponents@ri,"Area"][[1,2]]/Times@@ImageDimensions[ri])*Quantity[100,"micrometer"]*Quantity[50,"micrometer"]

Quantity[1933.1247965494795, "Micrometers"^2]