4

I am trying to optimize a function which involves NDSolveValue, but I cannot complete the optimization due to a memory leak. As mentioned in Memory leak with NDSolve, the memory leak might be due to a bug, but I am trying to break down my problem to see if I am doing some mistakes. I am using Mathematica 11.0.1.

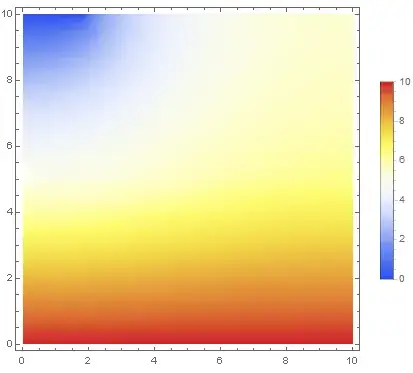
To illustrate my point, let us solve the 2D heat equation $\nabla \cdot \left[ \kappa ( \boldsymbol{r} ) \nabla T( \boldsymbol{r} ) \right] = \partial_x \left[ \kappa ( \boldsymbol{r} ) \partial_x T( \boldsymbol{r} ) \right] + \partial_y \left[ \kappa ( \boldsymbol{r} ) \partial_y T( \boldsymbol{r} ) \right] = 0$ using some arbitrary region, boundary conditions and a piecewise function $\kappa$:

area = Rectangle[{0, 0}, {10, 10}];
kappa[x_, y_] := Piecewise[{{5, y <= 5}, {10, 5 < y}}];
op = D[kappa[x, y]*D[u[x, y], x], x] + D[kappa[x, y]*D[u[x, y], y], y];

sol = NDSolveValue[
   {op == 0,
    DirichletCondition[u[x, y] == 10, y == 0],
    DirichletCondition[u[x, y] == 0, y == 10 && x < 2]},
    u,
    {x, y} ∈ area];

DensityPlot[sol[x, y], {x, y} ∈ area, Mesh -> None, 
 ColorFunction -> "TemperatureMap", PlotRange -> All, 
 PlotLegends -> Automatic]

with the output:

enter image description here

I am completely satisfied with the result, but some global variables have been generated during the calculation:

Names["Global`*"]

with the output:

{area, kappa, op, s5, s6, s7, s8, sol, u, x, y}

I do not understand where these s5, s6, s7 and s8 come from! After running the code multiple times, more and more global variables are generated. After five times, the output is:

{area, kappa, op, s12, s13, s14, s15, s18, s19, s20, s21, s24, s25, s26, s27, s30, s31, s32, s33, s5, s6, s7, s8, sol, u, x, y, y$}

My question is if this can cause me any memory problems? In my actual code, around 80 global variables are generated for each calculation and I guess that around 1000 calculations has to be done during my optimization. I have tried to use Remove[s5,s6,...], but it does not seem to release any memory, but maybe this large number of variables causes me some other problems?

If I define kappa to be a constant, no additional variables are generated. What can I do to the code to avoid the generation of these global variables?

Community
  • 1
Jens Rix
  • 81
  • 3
  • The kernel seems to be generating temporary variables. Weird, I haven't seen this before, and can't reproduce with similar code. I suspect it has to do with the Piecewise[] function. – Feyre Oct 25 '16 at 11:59
  • Looks like NDSolve creates symbols with Unique["s"] in processing the discontinuities. It should be considered a bug. It shouldn't be causing a significant memory leak, though, since it appears they are used only as symbols. – Michael E2 Oct 25 '16 at 12:26
  • @MichaelE2, pretty good analysis. I have a fix in place and if all goes well the next release will behave better - no more "sXY" symbols. Thanks! That said though, I wonder if this is really all that's to the memory issue. Jens, perhaps you could show in some more detail the actual optimization that you do? – user21 Oct 25 '16 at 18:47
  • @user21, no it is not all that is to the memory issue. But I temporarily fixed it by upgrading to a better computer and by extracting calculated points in my NMinimize and inserting these as InitialPoints in a new NMinimize when I am out of memory. The module that I minimize involves NDSolveValue, and my guess is still that the memory leak is due to the issue discussed in link. I will return if my temporary solution would not do it. – Jens Rix Oct 27 '16 at 10:11
  • @JensRix, if you find the time it were good if you could send it to the tech support then a developer could look at it and see if these are really the same issues. Unreported bugs have a close to zero chance of getting fixed. – user21 Oct 27 '16 at 11:25

1 Answers1

5

It appears the developers forgot to Remove the symbols, which are created with Unique:

area = Rectangle[{0, 0}, {10, 10}];
kappa[x_, y_] := Piecewise[{{5, y <= 5}, {10, 5 < y}}];
op = D[kappa[x, y]*D[u[x, y], x], x] + D[kappa[x, y]*D[u[x, y], y], y];

Trace[
 NDSolveValue[{op == 0, DirichletCondition[u[x, y] == 10, y == 0], 
   DirichletCondition[u[x, y] == 0, y == 10 && x < 2]}, 
  u, {x, y} ∈ area],
 _Unique | _Remove,
 TraceForward -> True,
 TraceInternal -> True]

Mathematica graphics

The symbols s5 etc. seemed to be used only for symbolic processing, e.g., to construct this function:

Mathematica graphics

Their creation should not use much memory, but they should have been removed.

Michael E2
  • 235,386
  • 17
  • 334
  • 747