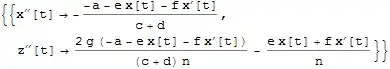2

I have a bunch of differential equations (nonlinear and linear) and some equality equations, all are in one cell. I want to use Mathematica to substitute the assigned values or variables into differential equations, and finally get a simplified version for them. As a simple example of my case is:

equations = {a == b1 + c*x''[t], b2 == d*x''[t] + e*(x[t]-y[t]) + f*(x'[t]-y'[t]),     
    g*y''[t] + e*(y[t] - x[t]) + f*(y'[t] - x'[t]) + m == 0, 
    n*z''[t] == m - R, R == 0, b1 == b2, y[t] == 2*x[t], 
    y'[t] == 2*x'[t], y''[t] == 2*x''[t]}

where I want to substitute the equivalent of y[t] and its derivatives and apply b1=b2 in the main first two equations and finally get a simplified result for x''[t] and z''[t]. I tried to use reduce as follows:

Reduce[{a == b1 + c*x''[t], b2 == d*x''[t] + e*(x[t]) + f*(x'[t]) , 
  g*y''[t] + e*(y[t] - x[t]) + f*(y'[t] - x'[t]) + m == 0, 
  n*z''[t] == m - R, R == 0, b1 == b2, y[t] == 2*z[t], 
  y'[t] == 2*z'[t], y''[t] == 2*z''[t]}, {x''[t], z''[t]}, {b1, b2,
   y[t], y'[t], y''[t],m}]

but, it does not work! it just give an answer for x''[t] which is: (a-e(x[t]-2*z[t])-f*(x'[t]-2*z'[t]))/(d+c).

similarly it should give a result for z''[t] as (-R+e*(x[t]-2*z[t])+f*x'[t]-2*z'[t]))/(2*g+n)

SPPearce
  • 5,653
  • 2
  • 18
  • 40
F R
  • 159
  • 8
  • What do you actually want? You can get a set of reduced conditions by replacing y everywhere using Reduce[equations /. y -> Function[{t}, 2 x[t]]] – SPPearce Oct 28 '16 at 10:10
  • the problem is that I have y[t]=2x[t] in the same cell as the rest of the differential equations, and this definition for y or other variables are changing in each example! so, I can't define it separately the way that you suggested since I have no information of the assigned values in this stage – F R Oct 28 '16 at 10:21
  • Are your constants (a,b,c etc) actually functions of t? – SPPearce Oct 28 '16 at 10:39
  • no, just x, y, z are function of time – F R Oct 28 '16 at 10:42

2 Answers2

1

So you have a set of equations that you wish to transform to differential equations in x''[t], and z''[t], without some of the other parameters. Solve will do that for you, if you specify the variables correctly:

Solve[equations, {x''[t], z''[t], y[t], y'[t], y''[t], b1, b2, m, R}]

Similarly you could Eliminate some parameters first 

Solve[Eliminate[equations, {b1, b2, m, R}], {x''[t], z''[t], y[t],y'[t], y''[t]}]

If the variables that need eliminating are consistent across the different cases then that should hopefully work. But I suspect that you want to be able to say Solve[equations,{x''[t],y''[t],z''[t]}], and not have to specify which parameters.

With only 11 free parameters, we can calculate all 330 subsets of 4 and try them all:

elimSets = Subsets[Select[Variables[(equations /. Equal -> Subtract)],FreeQ[#, t] &], {4}];
solveSets= Map[Solve[Eliminate[equations, #], {x''[t],z''[t],y[t],y'[t],y''[t]}] &, elimSets]

Some number of these may be the correct elimination for how you wish the ODEs to look.

SPPearce
  • 5,653
  • 2
  • 18
  • 40
  • Thanks for your comment, but not really. My question is related to substituting some assigned variables, and simplifying differential equations. I don't want a result for variables of ODE. – F R Oct 28 '16 at 12:13
  • @FaribaRahimi, completely changed my answer, does this help? – SPPearce Oct 28 '16 at 13:57
  • Thanks for your answer, but not really it did not help since I get the below results in using solve and eliminiate respectively: solve:

    Solve[{a == b1 + cx1''[t], b2 == dx2''[t] + e(x2[t] - y[t]) + f(x2'[t] - y'[t]) , gy''[t] + e(y[t] - x2[t]) + f(y'[t] - x2'[t]) + m == 0, nz''[t] == m - R, b1 == b2, x2[t] == x1[t], x2'[t] == x1'[t], x2''[t] == x1''[t], y[t] == 2z[t], y'[t] == 2z'[t], y''[t] == 2*z''[t]}, {x1''[t], z''[t]}, {b1, b2, x2[t], x2'[t], x2''[t], y[t], y'[t], y''[t], m}]

    out={{z''[t] -> -((-a + R)/(2 g + n)) - ((c + d) x''1[t])/(2 g + n)}}

     – F R Oct 31 '16 at 17:01
  • eliminate: Solve[eliminate[equations, y''[t] == 2*z''[t]}, {b1, b2, x2[t], x2'[t], x2''[t], y[t], y'[t], y''[t], m}], {x1''[t], z''[t]}]

    out=Solve[eliminate[{a == b1 + c (x1''[t], b2 == e (x2[t] - y[t]) + f (x2'[t] - y'[t]) +d (x2''[t],m + e (-x2[t] + y[t]) +f (-x2'[t] + y'[t]) +g y''[t] == 0,n z''[t] == m - R, b1 == b2, True,x2'[t] == x1'[t], x2''[t] == (x1''[t], y[t] == 2 z[t],y'[t] == 2 z'[t], y''[t] == 2 z''[t]}, {b1, b2, x2[t],x2'[t], x2''[t], y[t],y'[t], y''[t], m}], {( x1''[t], z[t]}] it does not give the results that I am after!

     – F R Oct 31 '16 at 17:04
  • @FaribaRahimi The eliminate should be Eliminate, remember Mathematica is case-sensitive. And, you forgot to clear the variables. (See the True in your code?) Execute Clear["`*", Derivative] and retry. If you want to know more about why you need to do this, check this post. – xzczd Nov 01 '16 at 03:26
  • Thanks a lot :) it worked this way – F R Nov 01 '16 at 15:17
0

Well, actually you're just one step beyond the answer. 

equations = {a == b1 + c*x''[t], b2 == d*x''[t] + e*(x[t] - y[t]) + f*(x'[t] - y'[t]), 
   g*y''[t] + e*(y[t] - x[t]) + f*(y'[t] - x'[t]) + m == 0, n*z''[t] == m - R, R == 0, 
   b1 == b2, y[t] == 2*x[t], y'[t] == 2*x'[t], y''[t] == 2*x''[t]};

Solve[equations, {x''[t], z''[t]}, {b1, b2, R, y[t], y'[t], y''[t], m}]

Mathematica graphics

The key points are:

  1. There're 9 equations inside equations, but you only need to solve for 2 unknowns, so you need to eliminate 7 of them.

  2. Solve also owns a hidden syntax similar to Reduce.

BTW you may also want to read this.

Community
  • 1
xzczd
  • 65,995
  • 9
  • 163
  • 468