Triangulate a surface given as a MeshRegion

Question

Suppose I have a surface given as a MeshRegion. Example:

r = DiscretizeRegion[RegionBoundary@Cuboid[], MaxCellMeasure -> Infinity, 
 MeshCellStyle -> {1 -> Black}]

{RegionDimension[r], RegionEmbeddingDimension[r]}
(* {2, 3} *)

How can I triangulate the faces, or refine an exsiting triangulation, so that each face would look similar to this below?

I know that I can in principle I can do something like this:

MeshRegion[
  RegionBoundary[
   TriangulateMesh@
    DiscretizeRegion[Cuboid[], MaxCellMeasure -> Infinity]],
  MeshCellStyle -> {1 -> Black}
]

But this will triangulate the whole 3D volume. I was wondering if there is a way that avoids this. Also, some of the surfaces I have won't easily convert to a BoundaryMeshRegion that can be triangulated in 3D (e.g. because the surface may not be closed).

An alternative starting point could be triangle-based instead of quadrangle based:

r = DiscretizeRegion[RegionBoundary@Cylinder[], 
  MaxCellMeasure -> 0.1, PrecisionGoal -> 1]

score 9 · Accepted Answer · answered Oct 28 '16 at 21:16

9

Why not use DiscretizeRegion again but with a lower MaxCellMeasure?

mr = DiscretizeRegion[RegionBoundary[Cuboid[]], MaxCellMeasure -> ∞, 
  MeshCellStyle -> {1 -> Black}]

DiscretizeRegion[mr, MaxCellMeasure -> {2 -> .01}, MeshCellStyle -> {1 -> Black}]

answered Oct 28 '16 at 21:16

Greg Hurst

35,921
1
90
136

I really thought I tried that and it didn't work! Apparently I did something wrong. This is the useful answer for me because it preserves neighbourhood relations. Triangulating faces separately doesn't. If you look carefully at the images in the other answers, the subdivision of the cube edges isn't identical between faces either. With this method it is. – Szabolcs Oct 28 '16 at 21:19
@Szabolcs Ah yes I see what you are saying. Just as an FYI, you could always add an extra step after triangulating faces separately and fix that issue with RepairMesh[r2, "TJunctionEdges"]. – Greg Hurst Oct 28 '16 at 21:23
2

I didn't even consider this. Feeling a bit foolish now... – Simon Woods Oct 28 '16 at 21:28
@Szabolcs What version are you on? All 3 of those examples work for me on 11.0.0. – Greg Hurst Nov 02 '16 at 15:09
@ChipHurst I am sorry, I am stupid. I used MaxCellMeasure -> number instead of MaxCellMeasure -> {2 -> number}. Need more coffee ... won't comment today anymore before thinking things through 3 times. Yes, everything works correctly. – Szabolcs Nov 02 '16 at 15:10
@Szabolcs no worries! – Greg Hurst Nov 02 '16 at 15:58
BTW in case you're interested: the whole purpose of this question was to implement this (surfaces smoothening). – Szabolcs Nov 02 '16 at 15:59

score 7 · Answer 2 · answered Oct 28 '16 at 20:39

After a bit of spelunking I got this:

r = DiscretizeRegion[RegionBoundary@Cuboid[], 
   MaxCellMeasure -> Infinity, MeshCellStyle -> {1 -> Black}];

Needs["TriangleLink`"]

r2 = Region`Mesh`Triangulate3DFaces[r, TriangleTriangulate[#, "pqa0.01"] &]

{RegionDimension[r2], RegionEmbeddingDimension[r2]}
(* {2, 3} *)

The TriangleTriangulate documentation describes how to control the triangulation.

score 5 · Answer 3 · answered Oct 28 '16 at 17:59

This is a hack, but it does the trick. The problem is that you can't use TriangulateMesh on a 2D polygon embedded in 3D. One solution is to translate/rotate your polygon to the xy plane, triangulate, then reverse the transformation.

triangulate3DPolygon[Polygon[pts__], opts : OptionsPattern[]] := Module[
    {a, b, c, U, V, W, tr, trpgon, newpts, newpgns},
    (*The rotation matrix - http://math.stackexchange.com/a/856705 *)
    {a, b, c} = pts[[;; 3]];
    tr = a;
    {a, b, c} = # - a & /@ {a, b, c};
    {U, W} = {Normalize[b], Normalize[Cross[b, c]]};
    V = Cross[U, W];
    {U, V, W}.(# - tr) & /@ pts;
    trpgon = TriangulateMesh[
        DiscretizeGraphics[
            Polygon[Most /@ ({U, V, W}.(# - tr) & /@ pts)]],
            opts
            ];
    newpts = (Transpose[{U, V, W}].PadRight[#, 3] + tr) & /@  MeshCoordinates[trpgon];
    newpgns = MeshCells[trpgon, 2];
    {newpts, newpgns}
];

Options[triangulate2DMeshEmb3D] = {"OutputType" -> "MeshRegion"};
triangulate2DMeshEmb3D[mesh_,opts : OptionsPattern[
    {MeshRegion, TriangulateMesh, Graphics3D, triangulate2DMeshEmb3D}]
    ] :=Module[ {pgons, data, extracount, bag, pgonPrimitives, head, pts},
    pgons = MeshPrimitives[mesh, 2];
    data = triangulate3DPolygon[#, 
        Evaluate@FilterRules[{opts}, Options[TriangulateMesh]]] & /@ pgons;

    extracount = 0;
    bag = Internal`Bag[];
    pgonPrimitives = {};

    Do[
     pgonPrimitives = Join[
        pgonPrimitives,
        data[[n, 2]] /. Polygon[a__] :> Polygon[a + extracount]
     ];
     Do[
      extracount++;
      Internal`StuffBag[bag, pt],
      {pt, data[[n, 1]]}
      ];
     , {n, Length@data}
     ];
    head = Switch[OptionValue["OutputType"], "MeshRegion", MeshRegion, 
      "Graphics3D", Graphics3D@*GraphicsComplex];
    pts = Internal`BagPart[bag, All];
    Clear[bag];
    head[pts, pgonPrimitives, 
     Evaluate[FilterRules[{opts}, Options[head]]]]
];

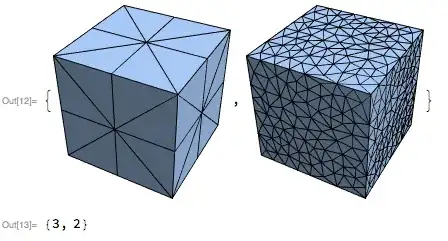
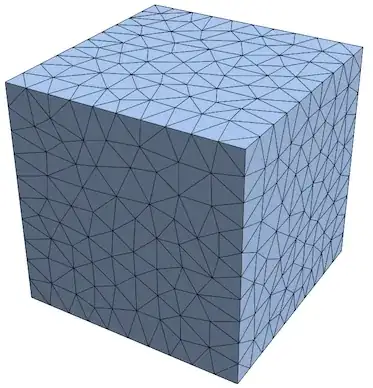
If you don't tell MeshRegion to color the lines in black, then you might think it didn't work,

But you can see that it does work, and the triangulation is customizable,

triangulate2DMeshEmb3D[
   msh,
   MeshCellStyle -> {1 -> Black},
   MaxCellMeasure -> #] & /@ {.2, .01}
Through[{RegionEmbeddingDimension, RegionDimension}[First@%]]

Triangulate a surface given as a MeshRegion

3 Answers3