Using EventLocator to detect periodic solutions in NDSolve

Question

I loop over some systems of DAEs with NDSolve; some solutions are periodic, some are not. When integrating with NDSolve, I integrate on {t,-1000,1000} starting from t=0 because I don't want to compute only one part of the non-periodic solutions. The problem is that when orbits are periodic, it computes the solution on several periods. To avoid this, I used EventLocator with the following testing function:

 isPeriodic[vals_, ic_] := (Norm[vals - ic] < .02) && (t < -1 || t > 1)

The 0.02 instead of 0 is due to numerical inaccuracies which makes the solution not perfectly periodic, but "almost". The condition t < -1 || t > 1 is used to prevent NDSolve from stopping immediately after starting ($f(0.000001)$ and $f(0)$ would trigger the periodicity condition since $\|f(0.000001)-f(0)\|$ is very likely to be lower than $0.02$).

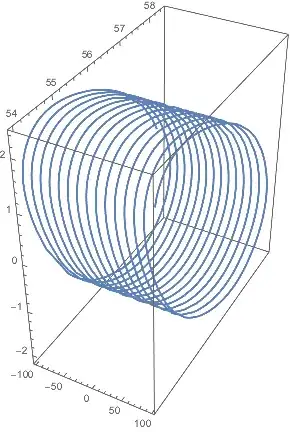
This works pretty well, except that I it returns the solution over two periods: $f(t)==f(0)$ is checked both for positive and negative t.

I could of course split the interval in two and keep only one part, but for some reasons I'd prefer to avoid that; additionally, it would avoid computing the periodic solution on two periods.

Full code, which may seem sligthly complex but is not really:

(* defines variables and system of DAE *)
vars = Array[s, 2];
varst = Through[vars[t]];
ic = {56.30672012303853`, 1.9416110387254666`};
sysDAE0 = {{0.2763932022500211` Sin[
        0.8090169943749473` (-s[1][t] + s[2][t])] Sin[
        0.3090169943749473` (s[1][t] + s[2][t])] + 
      0.7236067977499788` Sin[
        0.3090169943749473` (-s[1][t] + s[2][t])] Sin[
        0.8090169943749473` (s[1][t] + s[2][t])]} == {0}, 
   Derivative[1][s[1]][t]^2 + Derivative[1][s[2]][t]^2 == 
    1.`, {s[1][0], s[2][0]} == 
    ic, {Derivative[1][s[1]][0], 
     Derivative[1][s[2]][0]} == {-0.8903443552034469`, 
     0.45528774325404187`}};

(* test of periodicity *)    
isPeriodic[vals_, 
  ci_] := (Norm[vals - ci] < .02) && (t < -1 || t > 1)

(* solves the system *)
{solDAE} = 
 NDSolve[sysDAE0, vars, {t, -1000, 1000}, 
  Method -> {"EventLocator", "Event" -> isPeriodic[varst, ic],
                         "EventAction" :> Throw[Null, "StopIntegration"]}]
sol[t_] := Through[(vars /. solDAE)[t]];
{tmin, tmax} = Flatten@solDAE[[1]][[2, 1]];

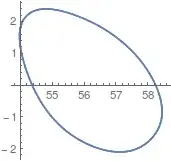
And the output, which is a closed curve (periodicity) plotted twice:

ParametricPlot[sol[t], {t, tmin, tmax}]

Question How to use events to compute only one period of the solution? One possibility would be to stop integration in both positive and negative t when the first periodicity condition is found, but "StopIntegration" does not do that (luckily).

Another possibility is to introduce a boolean boolPeriodic, turning it to True when the first periodic event is detected, and adding this boolean as an event to kill immediately the integration in the other direction (hence, avoiding computing a second time the period). But it does not help: it seems the EventLocator method is run in parallel for positive t and negative t. This is confirmed by adding a Print in the EventAction:

boolPeriodic = False; {solDAE} = 
 NDSolve[sysDAE0, vars, {t, -1000, 1000}, 
  Method -> {"EventLocator", 
    "Event" -> isPeriodic[varst, ic] || boolPeriodic, 
    "EventAction" :> Throw[boolPeriodic = True;Print["periodic"], "StopIntegration"]}]
sol[t_] := Through[(vars /. solDAE)[t]];

(* prints TWO "periodic" *)

Answer 1

Another way, stopping the forward integration if the backward integration is found to be periodic:

(*solves the system*)
periodicQ = False;
{solDAE} = NDSolve[{sysDAE0,
   WhenEvent[Evaluate@isPeriodic[varst, ic],
    periodicQ = True; "StopIntegration"],
   WhenEvent[Positive[t] && periodicQ,         (* was  t > $MachineEpsilon && periodicQ *) 
    "StopIntegration", "LocationMethod" -> "StepBegin"]},
  vars, {t, -1000, 1000}]
sol[t_] := Through[(vars /. solDAE)[t]];
{tmin, tmax} = Flatten@solDAE[[1]][[2, 1]];

ParametricPlot[sol[t], {t, tmin, tmax}]

Update note: First note that NDSolve integrates backwards from the initial condition to the beginning of the integration interval, if necessary, and next integrates forward from the IC to the end of the interval, if necessary. The event to stop forward integration in the case where a periodic solution was found in the backward integration was t > $MachineEpsilon, with an action to stop integration at the beginning of the step. I imagine it is extremely rare that the initial step in the forward integration would be less than $MachineEpsilon, but it's possible. Perhaps $MinMachineNumber is better. What would seem more exactly right is t > 0, but this is a special case in WhenEvent. It means that t changes from negative to positive. Since integration starts at t == 0, this event does not happen. However, Positive[t] is not a special case. It changes from False to True at the first step and so triggers an event. In general one might use Positive[t - t0] for an initial condition at t == t0.

---

Addendum: One can turn the solution into a periodic function, using the option PeriodicInterpolation and massaging the solution a little.

First I would change isPeriodic[] to be a little more accurate:

isPeriodic[vals_, ci_] := First[vals] == First[ci] && (Norm[vals - ci] < .02);

Then if you re-excute the code for solDAE we get much closer to an exact period:

{#["ValuesOnGrid"][[{1, -1}]], 
   Derivative[1][#]["ValuesOnGrid"][[{1, -1}]]} & /@ (vars /. solDAE)
(*
  {{{56.3067, 56.3067}, {-0.890345, -0.890344}},   <-- s[1]
   {{1.94161, 1.94161}, {0.455287, 0.455288}}}     <-- s[2]
*)

For PeriodicInterpolation to work, the first and last values have to be identical. They are close enough to replace the last one with the first one. The point t == 0. is also duplicated, because of the event stopping the forward integration. We need to delete it (with Most).

periodify[list_List] := ReplacePart[list, -1 -> First@list];

ClearAll[sol2];
sol2[t_] = Interpolation[Transpose@{
       Most@ #["Grid"],
       periodify@ Most@ #["ValuesOnGrid"],
       periodify@ Most@ Derivative[1][#]["ValuesOnGrid"]}, 
     PeriodicInterpolation -> True][t] & /@ (vars /. solDAE);

Here is a plot over several periods:

ParametricPlot3D[Evaluate@Flatten@{t, sol2[t]}, {t, -100, 100}, BoxRatios -> {1/2, 1, 1}]

Answer 2

It's not a perfect solution, but this does the trick:

(*solves the system*)
periodic = False;
{solDAE} = NDSolve[sysDAE0~Join~{WhenEvent[Evaluate@isPeriodic[varst, ic], 
           periodic = True; "StopIntegration"]}, vars, {t, -1000, 1000}]
sol[t_] := Through[(vars /. solDAE)[t]];
{tmin, tmax} = If[periodique==True,
             {0,sol["Domain"[]][[1,1,2]]},sol["Domain"[]][[1,1]]]

First, the code is rewritten with WhenEvent instead of the obsoleteEventLocator (cf Michael E2's comment). It introduces a boolean periodic; when the periodic event is detected, it triggers "StopIntegration" and also sets periodic to True. Then, it suffices to select half of the domain if the solution is periodic, and all of it otherwise. A last step would be to redefine the interpolating function on the right domain (instead of just saving the extremal values of it's parameter into two variables), but I don't know how to that yet.