Manipulate a function and a tangent

Question

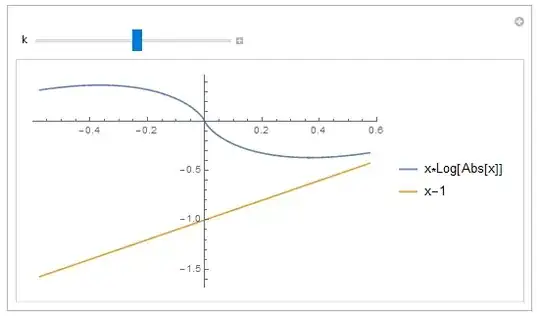
I know that the tangent at 0 of x Log [Abs [x]] is -Infinity. But this is not clearly visible on the curve at the scale x = -1 to x = 1.

Indeed, the convergence of the slope towards -Infinity is very slow.

I would really like to highlight this behavior thanks to an astute PlotRange coupled with a Manipulate which makes it possible to observe that the slope becomes infinite when looking at scales always.

I tried to do this:

Manipulate[
 Show[Plot[x *Log[Abs[x]], {x, (-10)^-k, 10^-k}, PlotRange -> All], 
  Plot[x - 1, {x, (-10)^-k , 10^-k}], PlotRange -> All], {k, -5, 5}]

but it returns an error message.

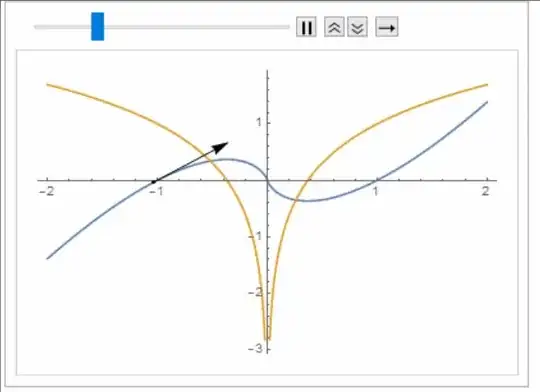
Do you want to plot the function f=x*Log[Abs[x]] or its derivative / slope? I dont see the derivative in your plot command. — Mauricio Fernández, Nov 12 '16 at 23:46
Possible duplicates: (18090), (119514). Related: (19737), (a79760) — Michael E2, Dec 13 '16 at 14:33

JimB · Answer 1 · 2016-11-13T00:15:08.030

1

I think you want -10^-k rather than (-10)^-k:

Manipulate[
 Show[Plot[x*Log[Abs[x]], {x, -10^-k, 10^-k}, PlotRange -> All], 
  Plot[x - 1, {x, -10^-k, 10^-k}], PlotRange -> All],
 {k, -5, 5}]

But it might be better if you had legends:

Manipulate[Plot[{x*Log[Abs[x]], x - 1}, {x, -10^-k, 10^-k},
  PlotRange -> All,
  PlotLegends -> {"x*Log[Abs[x]]", "x-1"}],
 {k, -5, 5}]

However, to get the "feeling" that the slope is $-\infty$ at $x=0$, you want both axes to be on the same scale:

Manipulate[Plot[x*Log[Abs[x]], {x, -10^-k, 10^-k}, AspectRatio -> 1,
  PlotRange -> {{-10^-k, 10^-k}, {-10^-k, 10^-k}}],
 {k, 0, 20}]

edited Nov 13 '16 at 00:15

answered Nov 12 '16 at 23:48

JimB

41,653
3
48
106

Thannnk you it'sperfect, I have been searching for a long time, Thanks a lot.Moreover, I am not sure, but I see that the slope becomes infinite when one looks at scales always smaller. Is ist a good impression ? – Robin Nov 12 '16 at 23:54
That's a good impression but that doesn't become as obvious if the axes are on different scales. I've edited my answer to make that more obvious. – JimB Nov 13 '16 at 00:16

score 1 · Answer 2 · answered Dec 13 '16 at 05:05

f[x_] := Piecewise[{{x Log[-x], x < 0}, {x Log[x], x > 0}}]
der[p_] := D[f[u], u] /. u -> p
fun[p_] := 
 Plot[Evaluate@{f[x], D[f[x], x]}, {x, -2, 2}, 
  Epilog -> {Point[{p, f[p]}], 
    Arrow[{{p, f[p]}, {p, f[p]} + Normalize[{1, der[p]}]}]}]
ListAnimate[Table[fun[j], {j, -2, 2, 0.12}]]

Manipulate a function and a tangent

2 Answers2