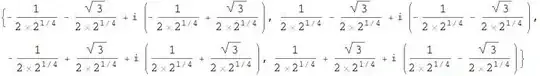Plotting complex solutions in Argand plane as arrows

Question

I have:

Clear[z]
Solve[z^4 == 1 - Sqrt[3] I, z] // ComplexExpand

Which produces these solutions:

{{z -> -(1/(2 2^(1/4))) - Sqrt[3]/(2 2^(1/4)) + 
    I (-(1/(2 2^(1/4))) + Sqrt[3]/(2 2^(1/4)))}, {z -> 
   1/(2 2^(1/4)) - Sqrt[3]/(2 2^(1/4)) + 
    I (-(1/(2 2^(1/4))) - Sqrt[3]/(2 2^(1/4)))}, {z -> -(1/(
     2 2^(1/4))) + Sqrt[3]/(2 2^(1/4)) + 
    I (1/(2 2^(1/4)) + Sqrt[3]/(2 2^(1/4)))}, {z -> 
   1/(2 2^(1/4)) + Sqrt[3]/(2 2^(1/4)) + 
    I (1/(2 2^(1/4)) - Sqrt[3]/(2 2^(1/4)))}}

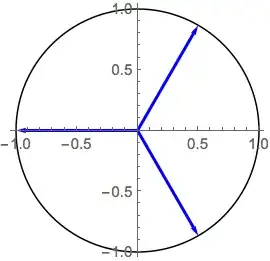
What would be the easiest way to convert these to a list of arrows to plot in the Argand plane. For example, the cube roots of -1:

Graphics[{
  Circle[],
  Blue, Thick,
  Arrow[{{0, 0}, {-1, 0}}],
  Arrow[{{0, 0}, {1/2, Sqrt[3]/2}}],
  Arrow[{{0, 0}, {1/2, -Sqrt[3]/2}}]
  }, Axes -> True, ImageSize -> Small]

Produces this image:

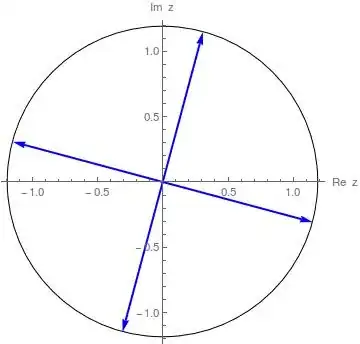
But I am looking for a cute way to convert all the data in the first problem, $z^4=1-\sqrt3 i$, into a list of arrows.

corey979 · Accepted Answer · 2017-01-06T00:15:30.160

9

sol = z /. Solve[z^4 == 1 - Sqrt[3] I, z] // ComplexExpand

coords = N @ ReIm @ sol (* N not needed, I just wanted a compact output *)

{{-1.14869, 0.307789}, {-0.307789, -1.14869}, {0.307789, 1.14869}, {1.14869, -0.307789}}

arr = Arrow[{{0, 0}, #}] & /@ coords

{Arrow[{{0, 0}, {-1.14869, 0.307789}}], Arrow[{{0, 0}, {-0.307789, -1.14869}}], Arrow[{{0, 0}, {0.307789, 1.14869}}], Arrow[{{0, 0}, {1.14869, -0.307789}}]}

For the circle:

{r = Abs[1 - Sqrt[3] I]^(1/4), N@r}

{2^(1/4), 1.18921}

Graphics[{Circle[{0, 0}, r], Blue, Thick, arr}, Axes -> True, 
 AxesLabel -> {"Re z", "Im z"}]

edited Jan 06 '17 at 00:15

answered Nov 14 '16 at 17:30

corey979

23,947
7
58
101

1

This is a really well explained explanation. I'd like to thank you for all the intermediate steps. They greatly helped my understanding. – David Nov 14 '16 at 19:11
I'm glad I could help :) – corey979 Nov 14 '16 at 21:30
1

I just made a simplifying edit; if you do not like this revert the change or edit as you see fit. IMHO multiple baroque alternatives do not enhance this otherwise concise answer. – Mr.Wizard Nov 20 '16 at 19:02

score 4 · Answer 2 · answered Nov 15 '16 at 05:12

Really just for fun to illustrate the geometric effect: $z^n=c$

f[c_, n_] := 
 Table[ReIm@N[Abs[c]^(1/n) Exp[Arg[c] I/n + 2 Pi I j/n]], {j, 0, n - 1}]
Manipulate[
 Module[{roots = f[Complex @@ p, n]},
  Graphics[{Circle[], Red, Circle[{0, 0}, Norm@p], Arrow[{{0, 0}, p}],
     Blue, Arrow[{{0, 0}, ##}] & /@ roots, Pink, Opacity[0.5], 
    Disk[{0, 0}, 0.5, {0, Arg[Complex @@ p]}],
    LightBlue,
    Disk[{0, 0}, Norm@p, {0, ArcTan @@ roots[[1]]}]},
   PlotLabel -> 
    Style[StringForm["\!\(\*SuperscriptBox[\(z\), \(`1`\)]\)=`2`", n, 
      Complex @@ p], 20],
   Axes -> True,
   PlotRange -> Table[{-2, 2}, 2]
   ]],
 {{p, {1, 0}}, {-2, -2}, {2, 2}}, {n, Range[2, 7]}]

Selected examples:

Really nice example. I'm gonna have to study this one. Thanks ever so much for all of your responses. — David, Nov 15 '16 at 06:58

Plotting complex solutions in Argand plane as arrows

2 Answers2

Linked