I'm trying to numerically solve a system of 64 equations (see picture below for the equation, where Erf is the error function and Q is a 64 by 64 matrix). But typing every single equation seems very tedious. So I was wondering (more like hoping) if there is some way to implement this formula in mathematica without explicitly typing all the equations, i.e. using the notion below somehow with e.g. NDSolve?
Asked
Active
Viewed 576 times
4
Michael E2
- 235,386
- 17
- 334
- 747
holistic
- 2,975
- 15
- 37
3 Answers
6
NDSolve can work with this in vector form .. see Vector form using NDSolve
n = 64;
lam = .2;
mu = 3;
Q = RandomReal[1, {n, n}];
vf[x : {_?NumberQ ..}] :=
Table[Sum[Q[[i, j]] x[[j]] + mu Q[[i, j]] x[[i]] x[[j]] , {j, n}] -
lam x[[i]], {i, 64}]
ic = Table[RandomReal[{-1, 1}], {n}];
vsoln = NDSolveValue[{x'[t] == Erf[vf[x[t]]], x[0] == ic}, x[t], {t, 0, 2}];
Plot[vsoln, {t, 0, 2}]
aside, I'm a bit annoyed I cant figure how to seperately style the output of the resulting vector valued interpolation function..except like this:
ListPlot[Transpose[Table[vsoln, {t, 0, 2, .01}]], Joined -> True,
DataRange -> {0, 2}]
george2079
- 38,913
- 1
- 43
- 110
4
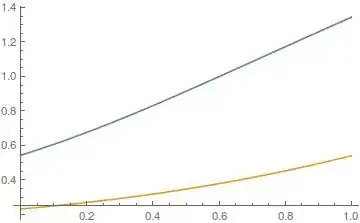
SeedRandom[1];
n = 2;
μ = RandomReal[];
λ = RandomReal[];
Q = RandomReal[1, {n, n}];
eq = Table[
x[i]'[t] ==
Erf @ Sum[Q[[i, j]] x[j][t] + μ Q[[i, j]] x[j][t] x[i][t], {j, 1, n}] - λ x[i][t], {i, 1, n}
]
ic = Table[x[i][0] == RandomReal[], {i, 1, n}]
sol = NDSolve[eq~Join~ic, Table[x[i][t], {i, 1, n}], {t, 0, 1}]
func = Table[x[i][t], {i, 1, n}] /. sol
Plot[func, {t, 0, 1}]
Works fine when n = 64:
In your real problem you need to, of course, set the values of parameters of interest (i.e., change all RandomReals to what you want/need).
corey979
- 23,947
- 7
- 58
- 101
1
Here's another vector form, without any reference to components, and using Dot instead of Sum:
n = 20;
λ = 1/2;
μ = 3;
SeedRandom[0];
Q = RandomReal[1, {n, n}];
ic = Table[RandomReal[{-1, 1}], {n}];
vsoln = NDSolveValue[
{x'[t] == Erf[Q.x[t] + μ Q.x[t] x[t] - λ x[t]], x[0] == ic},
x, {t, 0, 2}];
ListLinePlot[vsoln, PlotRange -> All]

Michael E2
- 235,386
- 17
- 334
- 747
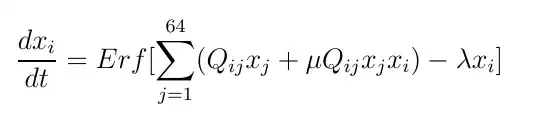



Qdefined beforehand; then you can useTableto construct aListof such equations. – corey979 Nov 18 '16 at 18:26