3

I will not be able to provide a simple minimum working example here as this seems to be very specific.

I have an interpolating function which I substituted into a PDE and then plot said PDE at a certain time for x and y.

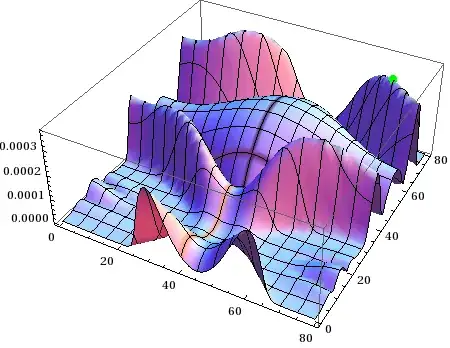
I'd like to find the global maximum of this function. Finding the maximum was described here. However, I find that this just finds the local maximum. As soon as the first maximum value is encountered, the FindMaximum or FindMaxValue are stopped and I don't get the global maximum.

For instance, when I run FindMaximum or FindMaxValue on the interpolating function that generates this:

enter image description here

The local maximum very close to the left bottom corner is returned as 1.7291*10^-6. Obviously the maximum is around 0.00002.

I have attached my .mat files here. The notebook that I use to plot and calculate maximum is as:

$HistoryLength = 0;

Needs["VectorAnalysis`"]
SetCoordinates[Cartesian[x, y, z]];
Needs["DifferentialEquations`InterpolatingFunctionAnatomy`"];
(*Loads the files*)
L = 79.5788;
fileList = FileNames["L_lambda_max_1wl_zg.mat", NotebookDirectory[]];
fileListxy = FileNames["L_lambda_max_1wl_zg.mat", NotebookDirectory[]];
fileListt = 
  FileNames["L_lambda_max_1wl_zg_time.mat", NotebookDirectory[]];
datat = Import[fileListt[[1]]];
trup = Max[Flatten[datat]];
tsrup = Ceiling[
   0.9 Flatten[Position[Ceiling[Flatten[datat]], Ceiling[trup]]]];
ts = tsrup[[1]];
dataxy = Import[fileListxy[[1]]];
solution = ListInterpolation[dataxy, {{0, L}, {0, L}, Flatten[datat]}];

(*Plots the data at 0.99 final time*)
Plot3D[
 solution[x, y, 0.99 datat // Flatten // Last], {x, 0, L}, {y, 0, L}, 
 PlotPoints -> 65]
fac datat // Flatten // Last



(*Defines EqS and plots it and finds the maximum*)
Clear[EqS, EqM]
fac = 0.6;
xg = 0.0
Bi = 1;
Bo = xg 1/300;
K1 = 1;
\[Epsilon] = 10^-6;
\[Delta] = 10^-3;
m = 2*0.025;
r = 0;
EqS = Div[(-h[x, y, t]^3)*Bo*Grad[h[x, y, t]]];


Res[x_, y_, t_] = Abs[EqS /. h -> solution];
EffectofG = 
 Plot3D[Res[x, y, fac datat // Flatten // Last], {x, 0, L}, {y, 0, L},
   MaxRecursion -> 2, PlotPoints -> 65, PlotRange -> Automatic]
FindMaxValue[{Res[x, y, fac datat // Flatten // Last], 0 <= x <= L, 
  0 <= y < L}, x, y]

(*Defines EqnM, plots it and finds the maximum *)

EqM = Div[m*(h[x, y, t]/(K1 + Bi*h[x, y, t]))^2*Grad[h[x, y, t]]];
Clear[ResM];
EqM;
Bi = 1;
K1 = 1;
\[Epsilon] = 10^-6;
\[Delta] = 10^-3;
m = 2*0.025;
r = 0;
ResM[x_, y_, t_] = Abs[EqM /. h -> solution];
EffectofM = 
 Plot3D[ResM[x, y, fac datat // Flatten // Last], {x, 0, L}, {y, 0, 
   L}, MaxRecursion -> 2, PlotPoints -> 65]
FindMaxValue[{ResM[x, y, fac datat // Flatten // Last], 0 <= x <= L, 
  0 <= y <= L}, x, y]

This was generated using a massive mathematica script and I don't think it would be to many people's interest to run the script for several hours to generate this data. Hence, I just uploaded the data.

Edit:

As per rm-rf's suggestion (see comments) I tried NMaximize with the following change in syntax.

I replaced:

FindMaxValue[{ResM[x, y, fac datat // Flatten // Last], 0 <= x <= L, 
  0 <= y <= L}, x, y]

with:

NMaximize[{ResM[x, y, fac datat // Flatten // Last]}, {x, y}]

I find that as I increase the value of fac in my code to say 0.99 times the end time, it gives me a LOCAL maximum instead of a GLOBAL maximum.

Community
  • 1
dearN
  • 5,341
  • 3
  • 35
  • 74
  • FindMaximum always tries to find only a local maximum, whereas NMaximize attempts to find a global maximum. Have you tried using NMaximize/NMinimize? – rm -rf Oct 16 '12 at 22:01
  • @rm-rf I tried NMaximize with NMaximize[{ResM[x, y, fac datat // Flatten // Last], 0 <= x <= L, 0 <= y <= L}, x, y] but it says that only 2 arguments are expected while I furnished 3. I need to furnish the arguments that I have... – dearN Oct 16 '12 at 22:11
  • I didn't mean to imply that you simply substitute one with the other. Did you read the documentation to check for the right syntax? Hint: NMaximize takes only 2 arguments – rm -rf Oct 16 '12 at 22:12
  • @rm-rf Yes I did read. I guess I don't get why its wrong. I see from the syntax that I need to specify x and y. Are you saying I don't need to specify the limits of x and y? – dearN Oct 16 '12 at 22:13
  • x and y are grouped as {x, y}, whereas you haven't in your call... See the third example for the syntax in the docs. I don't know if it'll work; just a guess. – rm -rf Oct 16 '12 at 22:14
  • @rm-rf No luck. I'll restart my kernel and check if all is well. – dearN Oct 16 '12 at 22:15
  • @rm-rf Just checked again. NMaximize still gives me a local maximum. – dearN Oct 16 '12 at 22:16
  • Oh well... was worth a shot. Can't play with it right now, but hopefully someone else can. – rm -rf Oct 16 '12 at 22:18
  • @drN Notice that you use fac once before defining it. If I run your notebook and then NMaximize[{ResM[x, y, fac datat // Flatten // Last], 0 <= x <= L, 0 <= y <= L}, {x, y}] I get {0.0000113102, {x -> 79.5788, y -> 79.5788}}. – b.gates.you.know.what Oct 16 '12 at 22:32
  • @b.gatessucks I'll try that out. You could post that as an answer though. – dearN Oct 16 '12 at 22:45
  • As an alternative, you might want to consider using FindAllCrossings2D[] on the appropriate derivatives of the function you want to optimize... – J. M.'s missing motivation Oct 17 '12 at 04:02

1 Answers1

8

I think the suggestion by @rm-rf works :

fac
(* 0.99 *)

sol = NMaximize[{ResM[x, y, fac datat // Flatten // Last], 0 <= x <= L, 0 <= y <= L}, {x, y}]
(* {0.000335995, {x -> 69.3566, y -> 71.9692}} *)

which agrees with the plot :

Show[Plot3D[ResM[x, y, fac datat // Flatten // Last], {x, 0, L}, {y, 0, L}, MaxRecursion -> 2, PlotPoints -> 65], 
     ListPointPlot3D[{{sol[[2, 1, 2]], sol[[2, 2, 2]], sol[[1]]}}, PlotStyle -> Directive[PointSize[Large], Green]]]

enter image description here

b.gates.you.know.what
  • 20,103
  • 2
  • 43
  • 84
  • You could also do something like Show[Plot3D[(* stuff *)], Graphics3D[{Green, Sphere[{sol[[2, 1, 2]], sol[[2, 2, 2]], sol[[1]]}, 2]}]]; adjust the radius of the Sphere[] as seen fit. – J. M.'s missing motivation Oct 17 '12 at 09:42