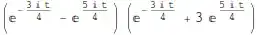4

I do not know why this method does not work for calculating the absolute value (or norm of (E^((-3 I t)/4) + 3 E^((5 I t)/4)) (E^((-3 I t)/4) - E^((5 I t)/4)));

f[t_] := (E^((-3 I t)/4) + 3 E^((5 I t)/4)) (E^((-3 I t)/4) - E^((5 I t)/4));
Refine[Abs@f[t], Assumptions -> {t > 0, t ∈ Integers}]
corey979
  • 23,947
  • 7
  • 58
  • 101
Unbelievable
  • 4,847
  • 1
  • 20
  • 46
  • Pardon me if I'm misunderstanding what you are doing. Aren't you trying to find the absolute value of a function? – Mirko Aveta Nov 26 '16 at 12:20

2 Answers2

6

There are several Q&A which show the use of ComplexExpand for this sort of task, such as this, this, this and so on, but I guess the different expressions in each case distinguish the questions from each other.

Perhaps one of these two forms would be acceptable:

Simplify@ComplexExpand[Abs@f[t]]
Simplify[%, t > 0]
(*
  2 Sqrt[2] Sqrt[5 + 3 Cos[2 t]] Sqrt[Sin[t]^2]
  2 Abs[Sin[t]] Sqrt[10 + 6 Cos[2 t]]
*)
Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747
4
f[t_] := (E^((-3 I t)/4) + 3 E^((5 I t)/4)) (E^((-3 I t)/4) - E^((5 I t)/4))

enter image description here

Sqrt @ FullSimplify @ Total @ ((ComplexExpand @ ReIm @ f[t])^2)

enter image description here

Thanks to Jack LaVigne I'd like to emphasize that the outer pair of round brackets (i.e., those enclosing the ...^2) are necessary: it appears that without them the squaring ^2 is done last, leading to an incorrect result.

Community
  • 1
corey979
  • 23,947
  • 7
  • 58
  • 101
  • Regarding the outer brackets, perhaps conventional function notation Total[x^2] would be the more natural choice here. – Simon Woods Nov 26 '16 at 21:34