I have matrix $$ A=\begin{bmatrix} 1 & 1\\1 & 0\\0 & 1 \end{bmatrix}$$ The question, similar to the discussion at Transform sphere to an ellipse in $\mathbb{R}^2$, is to find the parametric equation of the transformation of the unit circle with $T(x)=Ax$.
I showed that the transformation maps $R^2$ to a plane in $R^3$. The plane will be the column space of matrix $A$. Because the null space of the $A^T$ is the orthogonal complement of the column space of matrix $A$, I can do this:
A = {{1, 1}, {1, 0}, {0, 1}};
NullSpace[Transpose[A]]
Which gives this basis for the null space of $A^T$. $$\beta=\left\{ \begin{bmatrix} -1\\1\\1 \end{bmatrix}\right\}$$
Now I can do this:
Clear[x, y, z]
{x, y, z}.First[NullSpace[Transpose[A]]]
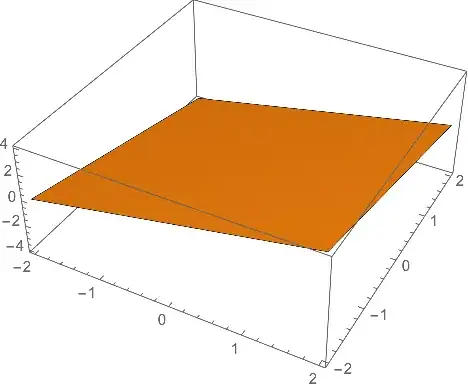
Which gives me the equation of the plane as $-x+y+z=0$. Solving for $z$ gives me $z=x-y$, so I can draw this transformation of $R^2$.
Plot3D[x - y, {x, -2, 2}, {y, -2, 2}, Mesh -> None]
Which gives this image:
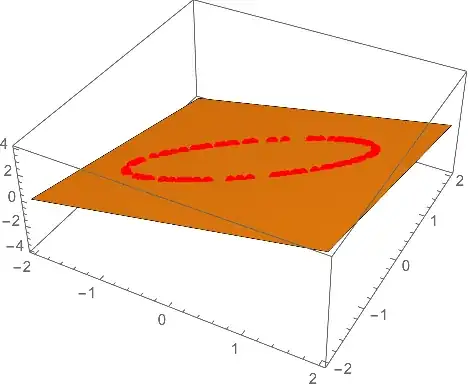
Next, I selected 100 random points from the unit circle (corey979's cool idea), then applied $T(x)=Ax$ to the set of points, using Michael E2's cool move.
pts = RandomPoint[Circle[], 100];
tpts = pts.Transpose[A];
Then I added these points to my image.
Show[
Plot3D[x - y, {x, -2, 2}, {y, -2, 2}, Mesh -> None],
Graphics3D[{
Red, PointSize[Large],
Point[tpts]
}]
]
So I have excellent visualization that the transformation maps the unit circle to an ellipse on the plane $-x+y+z=0$ in $R^3$.
But, now my question. How can I find a parametric equation representing this ellipse in the plane so I can use ParametricPlot3D to graph it?