Is it possible do a similar graphic (and animation) with Mathematica? (Please see the example of dataset on a sphere in this link). To see the rotating sphere, click on the "View the Interactive Sphere" button.
Asked
Active
Viewed 195 times
4
1 Answers
3
This is just to illustrate some ways utilizing resources from this site.
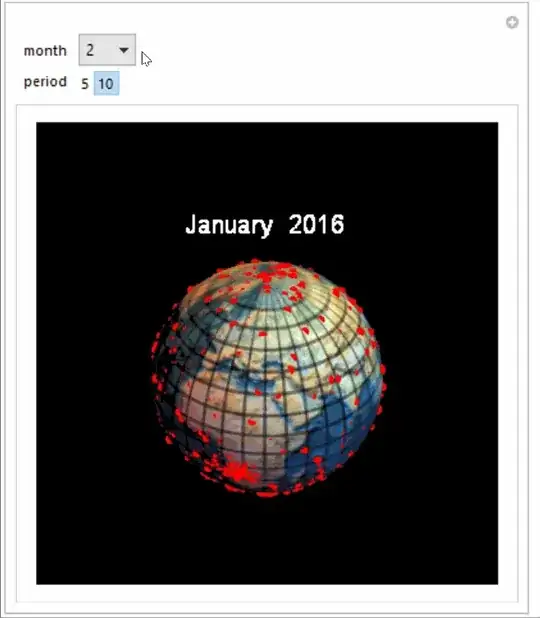
In the following I have just plotted earthquakes from December 2015 to earley 2016 with magnitude between 2.5 and 4 (for no particular reason).
Make Sphere
Code from here:
img = With[{\[CapitalDelta] = 30},
Row[Table[
GeoGraphics[GeoBackground -> GeoStyling["ReliefMap"],
GeoRange -> {{-90,
90}, {\[Lambda], \[Lambda] + \[CapitalDelta]}},
GeoProjection -> {"Equirectangular",
"Centering" -> {0, \[Lambda] + \[CapitalDelta]/2}},
ImageSize -> Small,
GeoGridLines -> Quantity[10, "AngularDegrees"],
GeoGridLinesStyle -> GrayLevel[0.4, 0.5]], {\[Lambda], -180,
180 - \[CapitalDelta], \[CapitalDelta]}]]]
pp = ParametricPlot3D[{Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]}, {u, 0,
2 \[Pi]}, {v, 0, \[Pi]}, Mesh -> None, PlotPoints -> 100,
TextureCoordinateFunction -> ({#4, 1 - #5} &), Boxed -> False,
PlotStyle -> Texture[img], Lighting -> "Neutral", Axes -> False,
RotationAction -> "Clip",
ViewPoint -> {-2.026774, 2.07922, 1.73753418}, ImageSize -> 300]
Autorotate
Code from here:
autoRotate[gr_Graphics3D, rate_: 5] :=
DynamicModule[{vp, va, vv, vc}, {vp, va, vv, vc} =
gr~AbsoluteOptions~#~OptionValue~# &@{ViewPoint, ViewAngle,
ViewVertical, ViewCenter};
Overlay[{Show[gr, SphericalRegion -> True, ViewPoint -> Dynamic[vp],
ViewAngle -> Dynamic[va], ViewVertical -> Dynamic[vv],
ViewCenter -> Dynamic[vc]],
Show[gr, Background -> Black, Boxed -> False,
SphericalRegion -> True,
ViewPoint ->
Dynamic[RotationMatrix[Clock[2 \[Pi], rate], vv].vp],
ViewAngle -> Dynamic[va], ViewVertical -> Dynamic[vv],
ViewCenter -> Dynamic[vc]]}, All, 1]]
Data The data is irrelevant as my point is to illustrate feasibility and one way.
ds = {DateList@#1, f[#2, #3], #4} & @@@ dat[[All, {1, 2, 3, 5}]];
ds = Reverse[ds];
gth = GatherBy[ds, {#[[1, 1]], #[[1, 2]]} &];
vp[a_, b_, c_] :=
{Text[Style[DateString[a, {"MonthName", " ", "Year"}],White, 20],
{0,0,1.5}],Red, PointSize[rs[c]], Point[b]};
gra = vp @@@ # & /@ gth;
anim = Show[Graphics3D[#], ppl] & /@ gra;
The data is grouped into earthquake locations and magnitudes by month and gra just makes a point at location with size scaled by magnitude.
An example visualization:
Manipulate[
autoRotate[anim[[month]], period],
{month, Range[13]}, {period, {5, 10}}]
EarthquakeData[]. – J. M.'s missing motivation Dec 10 '16 at 02:48