Parametric Region in polar coordinates

Question

I hope this helps at least one person who is in a similar situation. I am trying to create a region (suitable for solving a PDE on) which can be described through a Fourier cosine series in polar coordinates. That is

I used to be able to do this easily through the ParametricRegion command. Now that I am using Mathematica 11, however, I am having difficulty: when I use ParametricRegion with two parameters to create a region in polar coordinates, the region does not display correctly using the RegionPlot command e.g. try the following commands verbatim from the ParametricRegion documentation:

\[ScriptCapitalR] = ParametricRegion[{{s, (1 + t) s^2 - t}, -1 <= s <= 1 && 0 <= t <= 1}, {s, t}];
RegionPlot[\[ScriptCapitalR]]

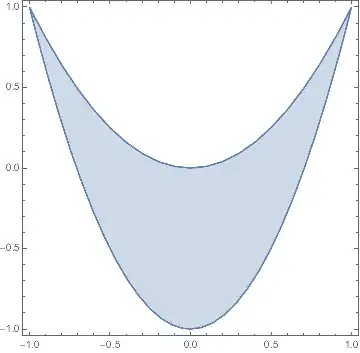
This code produces the following image:

This is not correct. I assume this is some kind of bug in Mathematica 11, because it worked fine in version 10. Does anyone know another/better way to create such a 2D region in polar coordinates; unfortunately, it is important for my application that I not use a polygonal approximation (the region must be smooth).

Thanks for any help!

Does DiscretizeRegion[reg] work for you? Or Needs["NDSolve`FEM`"]; emesh = ToElementMesh[reg]; MeshRegion[emesh]? (FWIW, the mesh regions actually make a polygonal approximation to the region.) — Michael E2, Dec 08 '16 at 03:49
Michael, Thanks for the help! in fact, the meshing works just fine (with occasional errors for some parameters), however, when I try to plot the result of solving the PDE (call it usol)
Plot3D[usol[x,y],{x,y} \[Element] \[CapitalOmega]]

it plots over a distorted region (like the one shown above). I suppose I might have to live with it for the time being. Just wondering if anyone has noticed this peculiarity yet. — PeterH, Dec 08 '16 at 03:56
Perhaps ElementMeshPlot3D might help. There are three answers in all using this undocumented function on site if you search for them. — Michael E2, Dec 08 '16 at 04:00

score 2 · Accepted Answer · edited Dec 08 '16 at 13:32

2

I can confirm that the OP code works in MM 10.4. Not sure if this is a bug, but as a workaround here is the conversion to ImplicitRegion that works in 11.0.1:

r = ImplicitRegion[
       RegionMember[
         ParametricRegion[{{s, (1 + t) s^2 - t}, -1 <= s <= 1 && 0 <= t <= 1}, {s, t}], {s, t}], {s, t}];
RegionPlot[r]

Mathematica graphics

edited Dec 08 '16 at 13:32

Michael E2

235,386
17
334
747

answered Dec 08 '16 at 13:30

Stitch

4,205
1
12
28

It works! Thank you for your help. – PeterH Dec 08 '16 at 14:58

Parametric Region in polar coordinates

1 Answers1