How to plot an equation solution and its derivative

Question

I've created an "ignorant code" using the functions I know.

Sure that there is a "smarter function" to solve what I need.

I think it's Solve, DSolve or RSolve that I should use, but I'm not sure how to structure it.

I have a circle equation:

$x^2+y^2=5$

Using Reduce I determine the minimum value and the maximum value of $x$ to meet the constraint $y> = 0$

Reduce[x^2 + y^2 == 5 && y >= 0, x]

$-\sqrt{5}\leq x\leq \sqrt{5}$

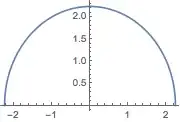
With the function below I applied a value for $Y$

Last[Solve[x^2 + y^2 == 5, y]] /. Rule -> Set

$\left\{\sqrt{5-x^2}\right\}$

This Plot represents the way a point can go

Plot[y, {x, -Sqrt[5], Sqrt[5]}, AxesLabel -> {"X", "Y"}, 
 PlotLegends -> {"\!\(\*FormBox[SqrtBox[\(5 - \*SuperscriptBox[\(x\), \
\(2\)]\)],
TraditionalForm]\)"}]

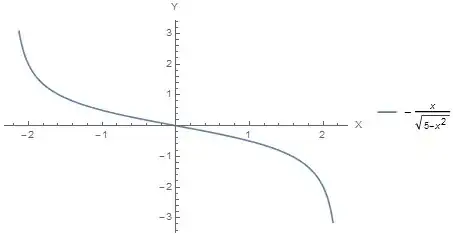
Here I present the equation of the point velocity on the path

velocidades = D[y, x]

$-\frac{x}{\sqrt{5-x^2}}$

If I am not mistaken this Plot represents the velocities of y with respect to the velocities of x

Plot[velocidades, {x, -Sqrt[5], Sqrt[5]}, AxesLabel -> {"X", "Y"}, 
 PlotLegends -> {"\!\(\*FormBox[\(-\*FractionBox[\(x\), SqrtBox[\(5 - \
\*SuperscriptBox[\(x\), \(2\)]\)]]\),
TraditionalForm]\)"}]

List with velocity values ​​of $X$

xVelocidade = Range[0.01, Sqrt[5], 0.01];

List with velocity values ​​of $Y$

yVelocidade = velocidades /. x -> # & /@ xVelocidade // N

I created a list where the first column are the velocities in $X$ and in the second column the velocities in $Y$

listVelocidades = Transpose[{xVelocidade, yVelocidade}]

I created a list with the proportions between the velocities in $Y$ in relation to the velocities in $X$

proporção = Abs[yVelocidade/xVelocidade];

In the previous list I looked for which value approaches "2". This is to identify where $y = 2x$

Nearest[proporção, 2]

The line below tells me which line is the most appropriate value

Position[proporção, First[%]]

$\left( \begin{array}{c} 218 \\ \end{array} \right)$

In the list with two columns I know where is the most appropriate proportion

velXvelY = 
 Extract[listVelocidades, 
  Position[proporção, First[Nearest[proporção, 2]]]]

$\left( \begin{array}{cc} 2.18 & -4.38108 \\ \end{array} \right)$

And finally, a test to verify

test = velXvelY[[1, 2]]/velXvelY[[1, 1]] // Abs

$2.00967$

Question:

I found an approximate value because of my limitations. What function would you find the exact value?

Answer 1

Here is one way to go about it:

sol[x_] := Solve[x^2 + y^2 == 5, y];
Y[x_] := y /. Last[sol[x]]
Plot[Y[x], {x, -Sqrt[5], Sqrt[5]}]
velocidades[x_] := D[Y[x], x]
Plot[Evaluate[velocidades[x]], {x, -Sqrt[5], Sqrt[5]}]

Regarding the reason for Evaluate see e.g. General::ivar is not a valid variable when plotting - what actually causes this and how to avoid it? or http://forums.wolfram.com/mathgroup/archive/2006/Mar/msg00232.html .

Looks like you want to solve $|\frac{dy}{dx}|=2$.

Solve[Abs[velocidades[x]] == 2 && -Sqrt[5] < x < Sqrt[5]]
(* {{x -> -2}, {x -> 2}} *)