I have the following function
(1/(35 \[Pi]^3 (-1 +
t^2)^13))65536 t (-(-1 + t) (1 + t) (363 + 10310 t^2 + 58673 t^4 +
101548 t^6 + 58673 t^8 + 10310 t^10 + 363 t^12) +
140 (1 + t^2) (1 + 48 t^2 + 393 t^4 + 832 t^6 + 393 t^8 + 48 t^10 +
t^12) Log[t]) (t - t^3 + (-1 + t^4) ArcTanh[t] +
t^2 (-4 PolyLog[2, t] + PolyLog[2, t^2]))^2
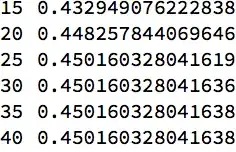
and would like to obtain a high-precision estimate of its integral over [0,1] (which I would then input, say to WolframAlpha, to check for a possible exact value). I've encountered numerical problems near t = 1.

RootApproximantwithToRadicals. – corey979 Dec 15 '16 at 07:55