How can I plot a line in three dimensions?

Question

I'm a newbie at Mathematica. I'm trying to build a line in three dimensions. The best I can do is to build two planes and get a line on the intersection of those planes, like this:

Plot3D[{y = 2 + x, z = 2 - x}, {x, -2, 2}, {y, -2, 2},
  ColorFunction -> "RustTones"]

It would be nice if someone also can share code showing how to build a line using two vectors.

= means you define y to be 2+x, you are essentially running {2 + x, 2 - x} — Feyre, Dec 19 '16 at 13:38

score 8 · Accepted Answer · answered Dec 19 '16 at 13:41

If you want to draw a complicated line, take a look at ParametricPlot3D

ParametricPlot3D[{x, 3 Sin[x], x^2}, {x, -1, 2}]

If you just want to draw a straight line, take a look at InfiniteLine

Graphics3D[{InfiniteLine[{2, 1, 1}]}, Axes -> True, AxesLabel -> {x, y, z}, Ticks -> Automatic]

score 5 · Answer 2 · answered Dec 19 '16 at 19:56

eq1 = y - x - 2;
eq2 = z + x - 2;

One can solve a system of equations

sol = {x, y, z} /. Solve[{eq1 == 0, eq2 == 0}, {x, y, z}]

{{x, 2 + x, 2 - x}}

to get the intersection in parametric form:

ParametricPlot3D[Evaluate@sol, {x, -2, 2}, PlotStyle -> {Thick, Red}]

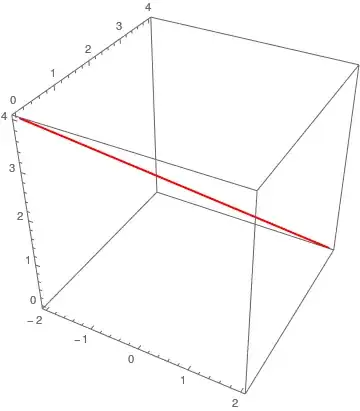
A different approach is to use Mesh functions:

ContourPlot3D[{eq1 == 0, eq2 == 0}, {x, -2, 2}, {y, -2, 2}, {z, -2, 
  6}, MeshFunctions -> {Function[{x, y, z, f}, eq1 - eq2]}, 
 MeshStyle -> {Thick, Red}, Mesh -> {{0}}, 
 ContourStyle -> Directive@{Opacity[0.5]}]

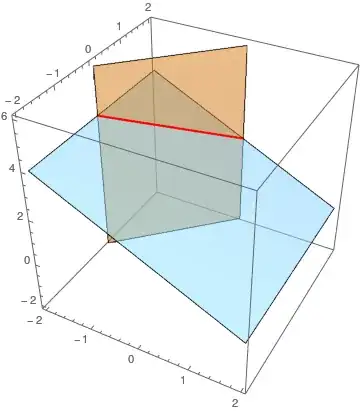
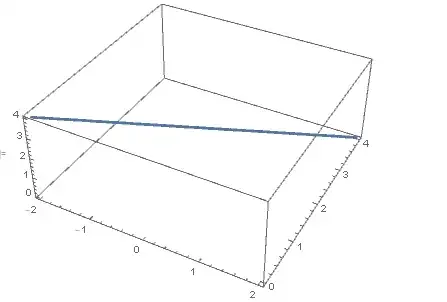
One can fade the surfaces completely to have only the highlighted intersection left:

ContourPlot3D[{eq1 == 0, eq2 == 0}, {x, -2, 2}, {y, -2, 2}, {z, -2, 
  6}, MeshFunctions -> {Function[{x, y, z, f}, eq1 - eq2]}, 
 MeshStyle -> {Thick, Red}, Mesh -> {{0}}, 
 ContourStyle -> Directive@{Opacity[0]}, BoundaryStyle -> Transparent]

Regarding your last example: see this. – J. M.'s missing motivation Dec 20 '16 at 04:47 — J. M.'s missing motivation, Dec 20 '16 at 04:47

score 4 · Answer 3 · answered Dec 19 '16 at 13:43

You could use the equation to generate points and use ListPointPlot3D:

y[x_] := 2 + x;
z[x_] := 2 - x;
ListPointPlot3D[Table[{x, y[x], z[x]}, {x, -2, 2, 0.01}]]

You could use a Graphics3D with Line (this is the one I would recommend, use Axes if you want Plot type axes):

Graphics3D[{Red, Line[{{-2, y[-2], z[-2]}, {2, y[2], z[2]}}]}]

How can I plot a line in three dimensions?

3 Answers3