Substitution and replacement in a matrix according to the position of an item in another matrix

Question

I have the following problem and obviously I need help

1) a list of choices --- in fact journals but this doesn't matter

votes = {
   {ff, tt, ii, "-", "-", "-"},
   {ii, tt, gg, dd, hh, ff},
   {ii, tt, gg, "-", "-", "-"},
   {ff, tt, ii, gg, dd, hh},
   {hh, ii, gg, "-", "-", "-"},
   {hh, ff, ii, "-", "-", "-"},
   {ff, tt, ii, hh, dd, gg},
   {tt, ff, "-", "-", "-", "-"},
   {gg, ii, "-", "-", "-", "-"},
   {dd, ii, tt, "-", "-", "-"},
   {gg, dd, tt, "-", "-", "-"},
   {ff, hh, ii, gg, tt, dd},
   {ff, ii, gg, hh, "-", "-"},
   {ff, gg, hh, tt, "-", "-"},
   {tt, "-", "-", "-", "-", "-"},
   {ii, dd, gg, ff, "-", "-"},
   {ii, hh, gg, tt, dd, ff},
   {ii, hh, tt, gg, "-", "-"},
   {tt, dd, ii, hh, gg, ff},
   {ii, hh, gg, "-", "-", "-"},
   {ff, gg, ii, "-", "-", "-"},
   {hh, tt, ii, gg, ff, dd},
   {ii, tt, dd, "-", "-", "-"},
   {ii, tt, gg, "-", "-", "-"},
   {dd, tt, ii, gg, ff, hh},
   {tt, dd, ii, gg, hh, ff},
   {gg, dd, ii, tt, ff, hh},
   {ii, tt, gg, dd, "-", "-"},
   {ff, tt, ii, "-", "-", "-"},
   {hh, ff, tt, "-", "-", "-"},
   {tt, ii, hh, gg, "-", "-"},
   {ii, gg, ff, tt, dd, hh}
   };

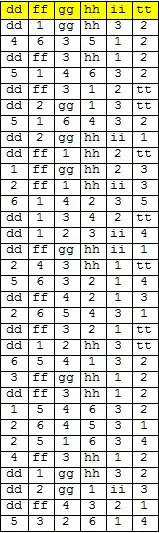
I have constructed a table

tab = Table[{dd, ff, gg, hh, ii, tt}, {i, 1, 33}]

The two tables seem to have the same structure but votes is about the preferences and tab about the ranking of the journals.

I want to substitute in tab, for each line, the true position of each item in the corresponding line of votes. For instance as the line 2 of votes is ii, tt, gg, dd, hh, ff in tab the second line must be 4, 3, 6, 5, 1, 2.

I have tried some thing like that

ReplacePart[tab, {6, 2} -> Position[votes[[6, All]], ff][[1, 1]]]

which, according to what I think to have understood, replaces the second element of the line 6 of tab by the position of ff in the line 6 of votes. But, I have not found how to iterate --- by functional programming --- or to loop by --- procedural programming --- on all elements of the table. For undocumented answers --- "-" ---, one can set a very large number.

Thanks for the help

I think there is a error in your example. Do you really mean that the result shoul be 4,3,6,5,1,2 ? — andre314, Dec 20 '16 at 11:30

andre314 · Answer 1 · 2016-12-20T19:57:20.953

4

ReplacePart works with named pattern, for example you can do :

ReplacePart[tab, {i_, 2} :> Position[votes[[i, All]], ff][[1, 1]]]

So, once you will have corrected the question, the definitve answer is :

res = ReplacePart[tab,
{i_, j_} :> (If[# =!= {}, #[[1, 1]], tab[[i, j]] ] & @
   Position[votes[[i, All]], tab[[i, j]]])];

res // Grid

Do not forget to use a delayed rule (:> instead of -> )

ReplacePart is not memory/speed optimal. It may be slow and memory consuming with large data sets.

I have followed your inital idea to use ReplacePart, but ReplacePart may not be the best approach.

edited Dec 20 '16 at 19:57

answered Dec 20 '16 at 09:56

andre314

18,474
1
36
69

Four nice answers that demonstrate the versatility of MA. – cyrille.piatecki Dec 21 '16 at 21:45

score 3 · Accepted Answer · answered Dec 20 '16 at 13:38

This can be done without explicitly creating tab for replacement.

tab = Function[{row},
  FirstPosition[row, #, #] & /@ {dd, ff, gg, hh, ii, tt} // Flatten] /@ votes

{{dd,1,gg,hh,3,2},{4,6,3,5,1,2},{dd,ff,3,hh,1,2},{5,1,4,6,3,2},{dd,ff,3,1,2,tt},{dd,2,gg,1,3,tt},{5,1,6,4,3,2},{dd,2,gg,hh,ii,1},{dd,ff,1,hh,2,tt},{1,ff,gg,hh,2,3},{2,ff,1,hh,ii,3},{6,1,4,2,3,5},{dd,1,3,4,2,tt},{dd,1,2,3,ii,4},{dd,ff,gg,hh,ii,1},{2,4,3,hh,1,tt},{5,6,3,2,1,4},{dd,ff,4,2,1,3},{2,6,5,4,3,1},{dd,ff,3,2,1,tt},{dd,1,2,hh,3,tt},{6,5,4,1,3,2},{3,ff,gg,hh,1,2},{dd,ff,3,hh,1,2},{1,5,4,6,3,2},{2,6,4,5,3,1},{2,5,1,6,3,4},{4,ff,3,hh,1,2},{dd,1,gg,hh,3,2},{dd,2,gg,1,ii,3},{dd,ff,4,3,2,1},{5,3,2,6,1,4}}

In the above the default when the position is not found has been set the symbol being searched for. In Mma Missing is generally used for missing values and most (if not all) of the functions know to ignore Missing values. For example, you could use Missing["NoVote"] as the default. Setting a default is optional.

Hope this helps.

score 1 · Answer 3 · answered Dec 20 '16 at 22:20

1

alts = {dd, ff, gg, hh, ii, tt};

ranks = Replace[alts, x_ :> (Position[votes[[#]], x]/. {{} -> x, {{n_}} :> n}), 1]& /@
    Range[Length@votes];

Grid[Join[{alts}, ranks], Dividers -> All, Background -> {None, {Yellow}}]

Mathematica graphics

answered Dec 20 '16 at 22:20

kglr

394,356
18
477
896

score 1 · Answer 4 · edited Apr 13 '17 at 12:55

Iterative use of Position as used by others is rarely the most efficient approach.⁽¹⁾

Here is a method that avoids Position (or FirstPosition) entirely.

fW[votes_, key_] :=
  Module[{z, RL = Range@*Length},
    z = ConstantArray[0, Dimensions @ votes];
    DeleteCases[votes, "-", {2}] /.
      AssociationThread[key, RL @ key] //
      MapIndexed[(z[[#2, #]] = RL[#];) &];
    z
  ]

Existing answer code as functions for comparison:

fEdmund[votes_, key_] :=
 Function[{row}, FirstPosition[row, #, #] & /@ key // Flatten] /@ votes

fkglr[votes_, alts_] :=
  Replace[alts, x_ :> (Position[votes[[#]], x] /. {{} -> x, {{n_}} :> n}), 1] & /@ 
   Range[Length@votes];

fandre[votes_, key_] :=
 Module[{tab},
  tab = ConstantArray[key, Length@votes];
  ReplacePart[
   tab, {i_, j_} :> (If[# =!= {}, #[[1, 1]], tab[[i, j]]] &@
      Position[votes[[i, All]], tab[[i, j]]])]
  ]

Timings:

First @ RepeatedTiming @ #[votes, {dd, ff, gg, hh, ii, tt}] & /@
  {fEdmund, fkglr, fandre, fW}

So my code is five times faster than the next best method.

Note:

I chose to output zeros in the place of blank votes because this makes more sense to me. If you prefer to have the vote items in the blanks you may replace the line

z = ConstantArray[0, Dimensions @ votes];

With:

z = ConstantArray[key, Length @ votes];

Substitution and replacement in a matrix according to the position of an item in another matrix

4 Answers4

Note: