Inserting columns multiple times

Question

I think this question is very simple and will be closed, but I'm left with doubts.

transform = CoordinateTransformData["Polar" -> "Cartesian", "Mapping"];
{p1, p2, p3, p4, p5, p6} = 
 transform[{2 Sqrt[3], # Degree}] & /@ Most[Subdivide[360, 6] + 30] //
   N

$\left( \begin{array}{cc} 3. & 1.73205 \\ 0. & 3.4641 \\ -3. & 1.73205 \\ -3. & -1.73205 \\ 0. & -3.4641 \\ 3. & -1.73205 \\ \end{array} \right)$

How could I apply the insert function to get this result?

Join[{{3., 1.7320508075688772, 0}, {0., 3.4641016151377544, 0}, {-3., 
   1.7320508075688772, 0}, {-3., -1.7320508075688772, 
   0}, {0., -3.4641016151377544, 0}, 
     {3., -1.7320508075688772, 0}}, {{3., 1.7320508075688772, 
   15}, {0., 3.4641016151377544, 15}, {-3., 1.7320508075688772, 
   15}, {-3., -1.7320508075688772, 15}, {0., -3.4641016151377544, 15}, 
     {3., -1.7320508075688772, 15}}]

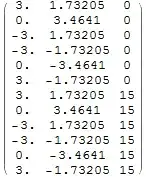
$\left( \begin{array}{ccc} 3. & 1.73205 & 0 \\ 0. & 3.4641 & 0 \\ -3. & 1.73205 & 0 \\ -3. & -1.73205 & 0 \\ 0. & -3.4641 & 0 \\ 3. & -1.73205 & 0 \\ 3. & 1.73205 & 15 \\ 0. & 3.4641 & 15 \\ -3. & 1.73205 & 15 \\ -3. & -1.73205 & 15 \\ 0. & -3.4641 & 15 \\ 3. & -1.73205 & 15 \\ \end{array} \right)$

I think there no solution with Insert only. Otherwise there are plenty of solutions. I would do something like this : Join[Insert[#, 0, -1] & /@ {p1, p2, p3, p4, p5, p6}, Insert[#, 15, -1] & /@ {p1, p2, p3, p4, p5, p6}] — andre314, Dec 20 '16 at 11:58

score 5 · Accepted Answer · edited Apr 13 '17 at 12:56

Using lowriniak's comment:

transform = CoordinateTransformData["Polar" -> "Cartesian", "Mapping"];
{p1, p2, p3, p4, p5, p6} = 
 transform[{2 Sqrt[3], # Degree}] & /@ Most[Subdivide[360, 6] + 30] //
   N

$\left( \begin{array}{cc} 3. & 1.73205 \\ 0. & 3.4641 \\ -3. & 1.73205 \\ -3. & -1.73205 \\ 0. & -3.4641 \\ 3. & -1.73205 \\ \end{array} \right)$

Through PadRight function:

Join[PadRight[{p1, p2, p3, p4, p5, p6}, {6, 3}], 
 PadRight[{p1, p2, p3, p4, p5, p6}, {6, 3}, {15}]]

$\left( \begin{array}{ccc} 3. & 1.73205 & 0 \\ 0. & 3.4641 & 0 \\ -3. & 1.73205 & 0 \\ -3. & -1.73205 & 0 \\ 0. & -3.4641 & 0 \\ 3. & -1.73205 & 0 \\ 3. & 1.73205 & 15 \\ 0. & 3.4641 & 15 \\ -3. & 1.73205 & 15 \\ -3. & -1.73205 & 15 \\ 0. & -3.4641 & 15 \\ 3. & -1.73205 & 15 \\ \end{array} \right)$

score 3 · Answer 2 · answered Dec 21 '16 at 22:05

Behold ArrayFlatten

pn = {p1, p2, p3, p4, p5, p6};

ArrayFlatten[{{pn, 0}, {pn, 15}}] // MatrixForm

$\left( \begin{array}{ccc} 3. & 1.73205 & 0 \\ 0. & 3.4641 & 0 \\ -3. & 1.73205 & 0 \\ -3. & -1.73205 & 0 \\ 0. & -3.4641 & 0 \\ 3. & -1.73205 & 0 \\ 3. & 1.73205 & 15 \\ 0. & 3.4641 & 15 \\ -3. & 1.73205 & 15 \\ -3. & -1.73205 & 15 \\ 0. & -3.4641 & 15 \\ 3. & -1.73205 & 15 \\ \end{array} \right)$

kglr · Answer 3 · 2016-12-21T22:59:44.260

3

Also

Distribute[{{0, 15}, pn}, List, List, List, Append[#2, #] &] // MatrixForm

or

Join @@ Outer[Append[#2, #] &,  {0, 15}, pn, 1] // MatrixForm

Note: you can use Insert[#2, #, -1] & instead of Append[#2, #] in the above.

edited Dec 21 '16 at 22:59

answered Dec 21 '16 at 22:36

kglr

394,356
18
477
896

Inserting columns multiple times

3 Answers3

Linked