27

What is the most painless way to sum over n variables, for example, if the range of summation is $i_1 < i_2 < i_3 < \dots < i_n$, where $n$ is an argument of the function in question?

Is there a package for this and more complex summation ranges?

I am not happy with programming loops all the time for this common summation range and if one has a large summation range, one cannot just use a combinat command to generate all subsets of a certain size, if this takes too much memory.

Example:

$$f(n)=\sum_{0 < i_1 < i_2 < \dots < i_n < 2n+1} \qquad \prod_{1\le r < s \le n} (i_s-i_r) $$

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
Phira
  • 755
  • 7
  • 13
  • So i1, i2 ...in are the ends of the ranges? What about the start of the ranges, always 1? What about variable naming (which variable will get those values)? – Sjoerd C. de Vries Jan 18 '12 at 10:30
  • 2
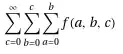
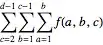
    Boole[] can sometimes be useful for complicated summations. – J. M.'s missing motivation Jan 18 '12 at 10:36
  • 1
    -1: This question is not particularly clear and could use some work (although the subject matter is interesting and welcome!). Can you give a more explicit example of the sums that you're interested in (the site supports LaTeX). Also, please codify all code... Once the question is edited, I'll remove my downvote. – Simon Jan 18 '12 at 12:34
  • Phira, the example sum you have given, which is the (unique) sum of all integer Vandermonde determinants in a certain range, does it have a closed form? Have you tried to identify the sequence from its first few terms using OEIS (or W|A)? – Simon Jan 19 '12 at 22:42

4 Answers4

20

You can write a few helper functions to help you. The following can probably be streamlined...

vars[s_String, n_Integer?Positive] := Table[Symbol[s <> ToString[i]], {i, 1, n}]
vars[sym_Symbol, num_] := vars[SymbolName[sym], num]

nestedRange[vars_List, min_, max_] /; min <= max := 
 Transpose@{vars, ConstantArray[min, Length[vars]], Append[Rest@vars, max]}

nestedSum[f_, vars:{__Symbol}, min_, max_] /; min <= max := 
 With[{r = Sequence @@ Reverse@nestedRange[vars, min, max]}, Sum[f, r]]
nestedSum[f_, {var:(_String|_Symbol), num_Integer?Positive}, 
 min_, max_] /; min <= max := nestedSum[f, vars[var, num], min, max]

Then, for example 

nestedSum[f[a, b, c], {a, b, c}, 0, Infinity] // TraditionalForm

produces screenshot

A larger sum is

In[]:= nestedSum[Total@vars[i, 4], {i, 4}, 1, 20] // Timing
Out[]= {0.016001, 371910}

which can be compared with evaluating the same thing using Boole

In[]:= v = vars[i, 4];
       With[{r = Sequence@@Table[{n, 1, 20}, {n, v}]}, 
            Sum[Boole[LessEqual@@v] Total@v, r]] // Timing
Out[]= {0.056003, 371910}
Simon
  • 10,167
  • 5
  • 57
  • 72
10

Here's another approach. With this solution you would enter the sum in the form sum[f, a0<a1<a2<=...<an], where you can use a mix of < and <= in the specification of the range of summation.

sum[f_, Less[b0_, a__, b1_]] := Sum[f, ##] & @@ 
  Reverse[MapIndexed[{#1[[1]], b0 + #2[[1]], #1[[2]] - 1} &, 
    Partition[{a, b1}, 2, 1]]]

sum[f_, LessEqual[b0_, a__, b1_]] := Sum[f, ##] & @@ 
  Reverse[MapThread[{#1, b0, #2} &, {{a}, Rest[{a, b1}]}]]

sum[f_, (ii : HoldPattern[Inequality[PatternSequence[_, 
   (Less | LessEqual)] .., _]])] := 
  Module[{lst, ops, vars, b0, b1, count},
   lst = List @@ ii;
   ops = lst[[2 ;; -1 ;; 2]] /. {Less -> 1, LessEqual -> 0};
   vars = lst[[;; -1 ;; 2]];
   Sum[f, ##] & @@ 
     Reverse[MapThread[{#1[[1]], lst[[1]] + #2, #1[[2]] - #3} &, 
       {Partition[Rest[vars], 2, 1], Accumulate[Most[ops]], Rest[ops]}
     ]
  ]]

So for example

sum[f[a, b, c], 0 < a <= b < c < d] // TraditionalForm

produces

Mathematica graphics

Heike
  • 35,858
  • 3
  • 108
  • 157
  • +1 Neater and more flexible than my hack! Dealing with the different inequality forms is annoying (I had similar issues here). It would be better if Mma made Less and LessEqual act as shorthand for the various Inequality[] constructions... – Simon Jan 19 '12 at 22:34
9

I will tackle the sum explicitly mentioned in your post.

Suppose you use i[1], i[2] and so on for iteration variables. The product can be formed as follows. -Subsets[Array[i, n], {2}] will form pairs. $i_s-i_r$ for $1\leqslant r<s\leqslant n$.

f[n_Integer?Positive] := Block[{i},
 Sum[Apply[Times, -Subtract @@@ Subsets[Array[i, n], {2}]], ##] & @@ 
  Reverse@Partition[Array[i, n + 1, 1] /. {i[n + 1] -> 2 n + 1}, 2, 1]]

The sequence $f_n$ grows rather fast:

In[79]:= {f[1], f[2], f[3], f[4], f[5], f[6]}

Out[79]= {3, 20, 588, 114048, 194347296, 3634840535040}
Sasha
  • 7,373
  • 36
  • 47
  • Does your function generate all the summands in memory or does it generate and sum them sequentially? – Phira Jan 18 '12 at 17:23
  • 2
    It generates them sequentially. This what Sum does for small enough explicit bounds. You can enforce this to always be the case for explicit integer limits with Method -> "Procedural" as documented on Sum's reference page. – Sasha Jan 18 '12 at 17:26
2

Here's how I would do it

i[0]=0;
T[n_]:=Table[{i[k],i[k-1]+1,2n+1},{k,1,n}];
f[n_]:=Sum[Product[i[s]-i[r],{r,1,n},{s,r+1,n}],Evaluate[Sequence@@T[n]]];
user1337
  • 1,068
  • 6
  • 13