Comparison of Continuous and discrete Fourier Transform

Question

Consider a continuous signal as follows:

wavesum = 1.6 Cos[t + 0.3] + 30.9 Cos[3 t - 1.5] + 2.8 Cos[7 t + 1.7] + 
          80.1 Cos[5 t + 2.1] + 5.5 Cos[9 t - 2.4];

The Fourier Transform of this will be

cft = Table[{(1/Pi)*
       Integrate[
       wavesum/E^(I*ω*t), {t, -Pi, Pi}], ω}, {ω, 
       1, 10}]; 

Now I extracted the frequency, amplitude and phase components of the constituent signals using the following code:

frequency = DeleteCases[cft, {a_, _} /; Abs[Chop[a]] == 0][[All, 2]];
amplitude = Abs[DeleteCases[cft, {a_, _} /; Abs[Chop[a]] == 0][[All, 1]]];
phase = Arg[DeleteCases[cft, {a_, _} /; Abs[Chop[a]] == 0][[All, 1]]];

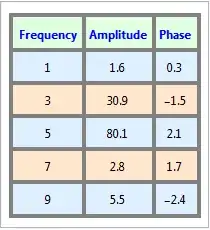
and displayed in a table format -

Panel@Grid[
Prepend[Transpose[{frequency, amplitude, phase}], 
Style[#, {Blue, Bold, 12}] & /@ {"Frequency", "Amplitude", 
 "Phase"}], Frame -> All, 
Dividers -> Directive[Gray, Thickness[4]], 
ItemSize -> {Automatic, 2}, 
Background -> {None, {LightGreen, {LightBlue, LightOrange}}}]

and the output is:

Now I sampled the signal to apply discrete Fourier Transform:

fs = 20;
n = 20;
nl = fs/2;
data = Table[wavesum, {t, 0, 1 - 1/n, 1/n}];

Then performed discrete Fourier Transform:

dft = Table[{Sum[
       data[[r]]/E^(2*Pi*I*(r - 1)*((s - 1)/n)), {r, 1, n}], s}, {s, 1, 
        nl}]; 

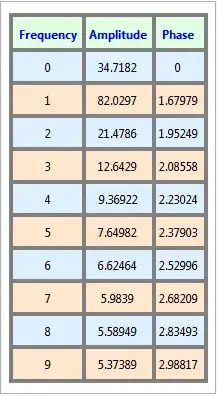
And got the frequency, amplitude and phase information -

freq = DeleteCases[dft, {a_, _} /; Abs[Chop[a]] == 0][[All, 2]] - 1;
amp = Abs[DeleteCases[dft, {a_, _} /; Abs[Chop[a]] == 0][[All, 1]]]/
nl;
pha = Arg[DeleteCases[dft, {a_, _} /; Abs[Chop[a]] == 0][[All, 1]]];

And displayed them:

Panel@Grid[
Prepend[Transpose[{freq, amp, pha}], 
 Style[#, {Blue, Bold, 12}] & /@ {"Frequency", "Amplitude", 
 "Phase"}], Frame -> All, 
Dividers -> Directive[Gray, Thickness[4]], 
ItemSize -> {Automatic, 2}, 
Background -> {None, {LightGreen, {LightBlue, LightOrange}}}]

However, if I choose the signal in the following format:

y = 1.6 Cos[2 π (t) + 0.3] + 30.9 Cos[2 π (3 t) - 1.5] + 
   2.8 Cos[2 π (7 t) + 1.7] + 80.1 Cos[2 π (5 t) + 2.1] + 
   5.5 Cos[2 π (9 t) - 2.4];

I get the desired result as I got for the continuous case.

What's wrong with my understanding and how can I fix it?