7

This ODE (#50 from Murphy's ODE collection book) causes kernel crash each time

enter image description here

Here is the code

ClearAll[y, x]
DSolve[ y'[x] == Cos[2 x] + (Sin[2 x] + y[x]) y[x], y[x], x]

Screen shot below. Should this be tagged a bug? Does this happen on other platforms? I am using windows 7. I tried it on 10.4, and it also crashes there.

Mathematica graphics

But on version 9.0, it does not crash, but it can't solve it:

Mathematica graphics

Maple can solve it, but solution is complicated using HeunC special functions which Mathematica do not have

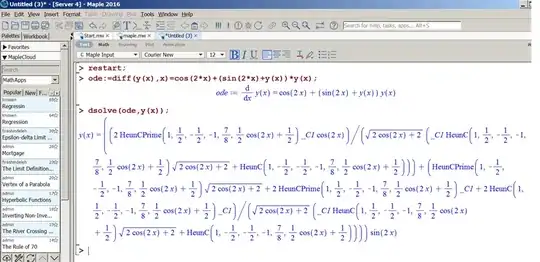
Mathematica graphics

But Book also gives one simple solution y(x)=tan(x), which is easily verified to be true by Mathematica. (the other solution it gives is little more complicated).

eq = Hold [D[y[x], x] == Cos[2 x] + (Sin[2 x] + y[x]) y[x]];
Simplify[ReleaseHold[eq /. y[x] -> Tan[x]]]

Mathematica graphics

Why does Mathematica kernel crash on this ODE?

Update:

Send bug report to Wolfram support, CASE:3806616 .

fyi, the book contains 2315 ODE's, which will take me long time to type and run. The current test report if you are interested is here. But it currently contains small number of ODE's from the book, will add more with time.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • 1
    Linux v11, get's stuck, but doesn't crash. – Feyre Dec 23 '16 at 20:21
  • 1
    The code crashes v10.3.1 and v11.0.0, both on Windows 64-bit – JungHwan Min Dec 23 '16 at 20:44
  • @Feyre what do you mean by 'stuck'? No solution or evaluation taking too long? For me, the code seems to crash the kernel 2-3 minutes after its evaluation. – JungHwan Min Dec 23 '16 at 20:46
  • @JungHwanMin I let it run for 10m, without result, I'm considering letting it run for an hour just to see if anything happens. It should be noted I have 16gb of RAM, which is still more than most today, which might have to do with it. – Feyre Dec 23 '16 at 20:56
  • I would go head and send a report to support@wolfram.com so that they can investigate and look address this. – ktm Dec 23 '16 at 21:22
  • It ran to completion giving Inverse warning, but not giving the solution. – Feyre Dec 23 '16 at 21:28
  • No crash (just a hang) for me on Mac v11. – Greg Hurst Dec 23 '16 at 21:32
  • I noticed when trying this on the Wolfram Cloud, version 11.3.0, it told me the computation was using too much memory, rather than taking too long. I guess Integrate is simply taking up too much memory when trying to calculate parts of it. – numbermaniac May 03 '18 at 12:04

1 Answers1

9

A bit too long for a comment. I think the hang is happening within Integrate:

Block[{Integrate},
  DSolve[y'[x] == Cos[2 x] + (Sin[2 x] + y[x]) y[x], y[x], x] /. {
    Integrate -> Inactive[Integrate]}
]

enter image description here

Edit

Here's the solution using withTimedIntegrate (as Micheal E2 pointed out in the comments):

withTimedIntegrate[DSolve[y'[x] == Cos[2 x] + (Sin[2 x] + y[x]) y[x], y[x], x], 1]

enter image description here

And just for fun, here's a way to solve this ODE:

  • Substitute y[x] == v'[x]/v[x] to get

    v''[x] - Sin[2x]v'[x] + Cos[2x]v[x] == 0

  • Next substitute Cos[x] == t to get

    (t^2 - 1)v''[t] + (2t^3 - t)v'[t] + (1 - 2t^2)v[t] == 0

  • Then substitute v[t] == t w[t] to get

    t(t^2 - 1)w''[t] + (2t^4 + t^2 - 2)w'[t] == 0

  • Substitute f[t] = w'[t] to get the first order separable equation

    t(t^2 - 1)f'[t] + (2t^4 + t^2 - 2)f[t] == 0

  • This equation is easily solved, and the solution is

    {{f[t] -> (E^-t^2 C[1])/(t^2 Sqrt[1 - t^2])}}

  • One can then perform all the back substitutions to get the final answer, which is where some nasty integrals will come into play.

Community
  • 1
Greg Hurst
  • 35,921
  • 1
  • 90
  • 136