RegionPlot3D example

Question

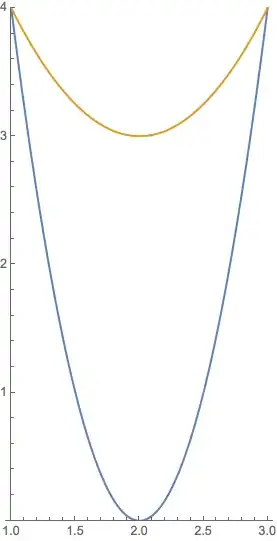
Can my colleagues demonstrate a couple of ways to use RegionPlot3D to draw the solid obtained by rotating the region bounded by the curves $y=4(x-2)^2$ and $y=x^2-4x+7$ around the $y$-axis?

Could you also obtain the volume using Mathematica's Volume and ImplicitRegion commands? The correct answer is $16\pi$.

Update: Here is a little explanation of my understanding of m_goldberg's z1[Sqrt[x^2 + y^2]] <= z <= z2[Sqrt[x^2 + y^2]], where $r=\sqrt{x^2+y^2}$.

Clear[r, z1, z2]
z1[r_] := 4 (r - 2)^2
z2[r_] := r^2 - 4 r + 7
Show[
 ParametricPlot3D[{RotationMatrix[\[Pi]/4, {0, 0, 1}].{r, 0, z1[r]}, 
   RotationMatrix[\[Pi]/4, {0, 0, 1}].{r, 0, z2[r]}}, {r, 1, 3}, 
  PlotStyle -> Thick],
 Graphics3D[{
   Arrow[{{0, 0, 0}, {3, 0, 0}}],
   Arrow[{{0, 0, 0}, {0, 3, 0}}],
   Arrow[{{0, 0, 0}, {0, 0, 4}}],
   {Opacity[0.5], InfinitePlane[{0, 0, 0}, {{1, 1, 0}, {0, 0, 1}}]},
   Red, Thick, PointSize[Large], 
   Arrow[{{2.5 Cos[\[Pi]/4], 2.5 Sin[\[Pi]/4], 0}, {2.5 Cos[\[Pi]/4], 
      2.5 Sin[\[Pi]/4], 4}}],
   Arrow[{{0, 0, 0}, {2.5 Cos[\[Pi]/4], 2.5 Sin[\[Pi]/4], 0}}],
   Black, 
   Text[Style["r", 12, Bold, Background -> White], {1.25 Cos[\[Pi]/4],
      1.25 Sin[\[Pi]/4], 0}],
   Text[Style["\!\(\*SubscriptBox[\(z\), \(1\)]\)(r)", 12, Bold, 
     Background -> White], {2.5 Cos[\[Pi]/4], 2.5 Sin[\[Pi]/4], 
     z1[2.5]}],
   Text[Style["\!\(\*SubscriptBox[\(z\), \(2\)]\)(r)", 12, Bold, 
     Background -> White], {2.5 Cos[\[Pi]/4], 2.5 Sin[\[Pi]/4], 
     z2[2.5]}]
   }],
 PlotRange -> {{0, 3}, {0, 3}, {0, 4}},
 PlotRangePadding -> None
 ]

I also thought this might help my students' understanding.

Manipulate[
 Show[ParametricPlot3D[{RotationMatrix[t, {0, 0, 1}].{x, 0, 
      4 (x - 2)^2}, 
    RotationMatrix[t, {0, 0, 1}].{x, 0, x^2 - 4 x + 7}}, {x, 1, 3}, 
   PlotStyle -> Thick],
  Graphics3D[{
    Arrow[{{0, 0, 0}, {3, 0, 0}}],
    Arrow[{{0, 0, 0}, {0, 3, 0}}],
    Arrow[{{0, 0, 0}, {0, 0, 4}}],
    Opacity[0.5], 
    InfinitePlane[{0, 0, 0}, {{Cos[t], Sin[t], 0}, {0, 0, 1}}]
    }],
  PlotRange -> {{-3, 3}, {-3, 3}, {0, 4}}, 
  PlotRangePadding -> None], {t, 0, 2 \[Pi]}
 ]

Answer 1

Taking the constraints that I guessed, 1<= x <= 3, as granted, the work proceeds as follows.

I am going to work first in the xz-plane and then rotate about the z-axis. I do this solely because I find it convenient.

z1[r_] := 4 (r - 2)^2 
z2[r_] := r^2 - 4 r + 7

Step 1 -- look at things in 2D. Always a good idea.

Plot[{z1[x], z2[x]}, {x, 1, 3},
 PlotRange -> {0, 4},
 AspectRatio -> Automatic]

Step 2 -- make 3D plot

Here is one way -- the fast and easy way. It is fast because it only plots the two bounding surfaces.

Show[
 RevolutionPlot3D[z1[r], {r, 1, 3}],
 RevolutionPlot3D[z2[r], {r, 1, 3}],
 BoxRatios -> {6, 6, 4},
 ImageSize -> Medium]

It can be with RegionPlot, too.

RegionPlot3D[
  z1[Sqrt[x^2 + y^2]] <= z <= z2[Sqrt[x^2 + y^2]], 
  {x, -3, 3}, {y, -3, 3}, {z, 0, 4},
  BoxRatios -> {6, 6, 4},
  PlotPoints -> 300]

Warning: the above plot takes minutes to render and rotating it with the mouse is painfully slow.

Step 3 -- make an implicit region and find its volume

impR = 
  ImplicitRegion[
    z1[Sqrt[x^2 + y^2]] <= z < z2[Sqrt[x^2 + y^2]] && -3 <= x <= 3 && -3 <= y <= 3, 
    {x, y, z}];

Volume[impR]

(113 π)/2 - 81 ArcSec[3] - 81 ArcSin[1/3]

π Rationalize[N[(113 π)/2 - 81 ArcSec[3] - 81 ArcSin[1/3]]/π]

16 π