Getting error NDSolve::bvdisc: when solving a differential equation

Question

I have the following code

ep = 80;
a = 10;
cb[1] = 0.001;
cb[2] = 0.001;
zf = 10;
z[1] = 1;
z[2] = -1;
cp[i_] = cb[i] Exp[-z[i] f[x]];

p = 
  NDSolve[
    {f''[x] == D[HeavisideTheta[x - 10], x] zf/(ep a^2) - 
                 1 Sum[z[i] cp[i], {i, 1, 2}], 
     f[10] == zf/(ep a^2), f'[20] == 0},
     f, {x, 10, 100 }, 
     MaxSteps -> Infinity, 
     InterpolationOrder -> All, 
     Method -> 
       {"Shooting", 
          "StartingInitialConidtions" -> {f[10] == zf/(ep a^2), f'[20] == 0}}]

When I execute the code, I get the following error message:

NDSolve::bvdisc: NDSolve is not currently able to solve boundary value problems with discrete variables. >>

Could you please tell me where I have made a mistake?

first thing you should do is verify you can solve an lnitial value problem (specify f'[10]) before attempting to use the shooting method. also for the shoting method the StartingInitialConditions are specified at the initial point (10) — george2079, Dec 31 '16 at 14:34
The problem lies with the delta function, D[HeavisideTheta[x - 10], x], but why NDSolve chooses to respond with this particular error message is not obvious to me. — bbgodfrey, Dec 31 '16 at 14:40

bbgodfrey · Answer 1 · 2017-01-01T17:06:11.160

5

Actually, simply

p = First@NDSolve[{f''[x] == - Sum[z[i] cp[i], {i, 1, 2}], 
    f[10] == zf/(ep a^2), f'[20] == 0}, f, {x, 10, 100 }];
Plot[(f /. p)[x], {x, 10, 100 }]

gives the same answer. The term D[HeavisideTheta[x - 10], x] zf/(ep a^2) has no effect, because it is at the boundary. It is strange that NDSolve gives an error instead of just ignoring the term.

edited Jan 01 '17 at 17:06

answered Dec 31 '16 at 17:10

bbgodfrey

61,439
17
89
156

Thanks alot, yes , the problem for me is why mathematica does not understand this. – amin bk Dec 31 '16 at 19:48
1

@aminbk it is difficult to say why Mathematica behaves as it does. I recommend that you focus on working around the problem, as I did in this particular case. Do you have a more general problem that you are trying to solve? – bbgodfrey Dec 31 '16 at 19:56

zhk · Answer 2 · 2017-01-01T04:37:01.007

4

This is more like a comment.

You have a discontinuous ode, so to turn off the discontinuity during NDsolve's processing of your ode with DiscontinuityProcessing,

NDSolve[{f''[x]==DiracDelta[-10 + x] zf/(ep a^2) - 1 Sum[z[i] cp[i], {i, 1, 2}],
f[10] == zf/(ep a^2), f'[20] == 0}, f, {x, 10, 100},
Method -> {"DiscontinuityProcessing" -> False}]

which generate this error,

NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 10.`.

So I added a submethod Method -> "ExplicitEuler"

p = NDSolve[{f''[x] == 
  DiracDelta[-10 + x] zf/(ep a^2) - 1 Sum[z[i] cp[i], {i, 1, 2}], 
  f[10] == zf/(ep a^2), f'[20] == 0}, f, {x, 10, 100}, 
  Method -> {"FixedStep", Method -> "ExplicitEuler", 
  "DiscontinuityProcessing" -> False}]

which produced a solution but with a warning,

NDSolve::nlnum: The function value {-0.0000234567,2.5*10^-6+0.00125 DiracDelta[0.]} is not a list of numbers with dimensions {2} at {x,f[x],(f^[Prime])[x]} = {10.,0.00125,-0.0000234567}.

Plot[f[x] /. p, {x, 10, 100}]

Edit

By now, we are sure that NDSolve has problems with DiracDelta. So there is another way to deal with it by approximating it by a NormalDistribution,

e1=0.00001;
p1 = NDSolve[{f''[x] == 
    PDF[NormalDistribution[10, e1], x] zf/(ep a^2) - 
     1 Sum[z[i] cp[i], {i, 1, 2}], f[10] == zf/(ep a^2), f'[20] == 0},
   f, {x, 10, 100}, MaxStepSize -> e1, 
  MaxSteps -> Infinity]

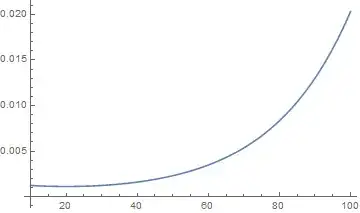
Finally, plotting the two results combine,

Show[Plot[f[x] /. p, {x, 10, 100}], 
 Plot[f[x] /. p1, {x, 10, 100}, PlotStyle -> {Dashed, Red}]]

Apparently, both numerical solutions p and p1 are identical.

edited Jan 01 '17 at 04:37

answered Dec 31 '16 at 15:05

zhk

11,939
1
22
38

@ MMM I am getting this error NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 10.?? – amin bk Dec 31 '16 at 19:46
@aminbk which part of the code is giving you this error? – zhk Jan 01 '17 at 03:45
@ MMM when I execute the code above I get the following error General::unfl: Underflow occurred in computation.General::stop: "Further output of !(* StyleBox[ RowBox[{"General", "::", "unfl"}], "MessageName"]) will be suppressed during this calculation" – amin bk Jan 01 '17 at 12:15
when I execute p1 = .... do you know what is the reason? – amin bk Jan 01 '17 at 12:17
@aminbk Sorry dear. I have no clue. What version of MMA you are using? I have V11.0. – zhk Jan 01 '17 at 13:02
I have version of 7 :( – amin bk Jan 02 '17 at 00:23
can I have your email address please?: – amin bk Jan 02 '17 at 13:42
@aminbk https://meta.stackexchange.com/questions/5234/how-does-accepting-an-answer-work – zhk May 02 '17 at 16:57

Mariusz Iwaniuk · Answer 3 · 2016-12-31T16:22:25.040

4

DiracDelta[x] can be replaced by:E^(-(Abs[x]/epsilon))/(2 epsilon) where epsilon is a sufficiently small real number,but not strictly zero.

p = With[{eps = 1/10^9}, 
NDSolve[{f''[x] == E^(-(Abs[-10 + x]/eps))/(2 eps)*zf/(ep a^2) - 
Sum[z[i] cp[i], {i, 1, 2}], f[10] == zf/(ep a^2), f'[20] == 0},f, {x, 10, 100}]];

Plot[f[x] /. p, {x, 10, 100}, AxesOrigin -> {10, 0}]

edited Dec 31 '16 at 16:22

answered Dec 31 '16 at 15:29

Mariusz Iwaniuk

13,841
1
25
41

Why the solution curve starts in the second quadrant? – zhk Dec 31 '16 at 16:07
1

@MMM. Problem is a Plot gives strange output.I'm edited answer. – Mariusz Iwaniuk Dec 31 '16 at 16:21

Getting error NDSolve::bvdisc: when solving a differential equation

3 Answers3