FEM Mesh for pipes and tubes

Question

I work with pipe systems and would like to use finite elements within NDSolve for regions inside or exterior to a pipe. How to do I make a mesh of the region interior or exterior to a complex pipe geometry. Here is a very simple geometry.

Needs["NDSolve`FEM`"];
L1 = 10;
L2 = 5;
r = 0.5;
R1 = 2;
p1 = ParametricPlot3D[{x, r Cos[θ], r Sin[θ]}, {x, 0, 
    L1}, {θ, -π, π}];
p2 = ParametricPlot3D[{L1 + Cos[t] (R1 + r Cos[u]), r Sin[u], 
    R1 + Sin[t] (R1 + r Cos[u])}, {t, -(π/2), 0}, {u, 0, 2 π}];
p3 = ParametricPlot3D[{L1 + R1 + r Cos[θ], r Sin[θ], 
    z + R1}, {z, 0, L2}, {θ, -π, π}];
Show[p1, p2, p3, PlotRange -> {{-5, L1 + 5}, {-5, 5}, {-5, L2 + 5}}]

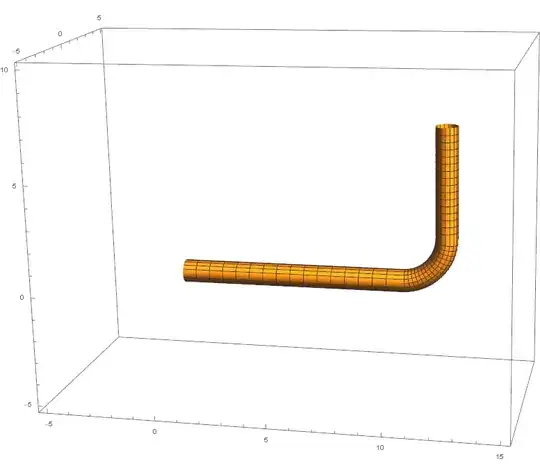
Mathematica graphics

How do I convert this into a mesh within the pipe or in a cuboid external to the pipe?

I have tried DiscretizeRegion but this only works for an ImplicitRegion. Do I have to turn my parametric region into an implicit region? Is there code for doing this? Are there other methods.

Edit 1

I have been working on using ImplicitRegion and have come up with the following

ir = ImplicitRegion[(0 <= x <= L1 && y^2 + z^2 == r^2) ||
   ((R1 - Sqrt[(x - L1)^2 + (z - R1)^2])^2 + y^2 == r^2 && 
     L1 <= x <= L1 + R1 + r && -R1 - r <= z <= R1) ||
   (R1 <= z <= L2 && y^2 + (x - L1 - R1)^2 == r^2),
  {x, y, z}];
DiscretizeRegion[ir, MaxCellMeasure -> 0.01 r]

Mathematica graphics

Clearly I need some helper functions that will return the implicit functions for general pipe and bend locations. Are there methods for this? Are there better methods than this?

Edit 2

Following the suggestion of user9490 (thank you) I continue with the parametric plots and fill in the ends.

Needs["NDSolve`FEM`"];
L1 = 10;
L2 = 5;
r = 0.5;
R1 = 2;
p1 = ParametricPlot3D[{x, r Cos[θ], r Sin[θ]}, {x, 0, 
    L1}, {θ, -π, π}];
p2 = ParametricPlot3D[{L1 + Cos[t] (R1 + r Cos[u]), r Sin[u], 
    R1 + Sin[t] (R1 + r Cos[u])}, {t, -(π/2), 0}, {u, 0, 2 π}];
p3 = ParametricPlot3D[{L1 + R1 + r Cos[θ], r Sin[θ], 
    z + R1}, {z, 0, L2}, {θ, -π, π}];
p4 = ParametricPlot3D[{0 , a Cos[θ], a Sin[θ]}, {a, 0, 
    r}, {θ, -π, π}];
p5 = ParametricPlot3D[{L1 + R1 + a Cos[θ], a Sin[θ], 
    L2 + R1}, {a, 0, r}, {θ, -π, π}];
g = Show[p1, p2, p3, p4, p5, 
  PlotRange -> {{-5, L1 + 5}, {-5, 5}, {-5, L2 + 5}}]

Mathematica graphics

Now I go on to make discretized graphics item

a = DiscretizeGraphics[
  Normal[g /. (Lighting -> _) :> Lighting -> Automatic]]

Mathematica graphics

This has worked but when I try to make a boundary mesh I get a poor quality mesh

b = ToBoundaryMesh[a, MaxCellMeasure -> 0.2 r];
b["Wireframe"]

Mathematica graphics

This is very clear if you zoom in

Show[b["Wireframe"], PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}]

Mathematica graphics

Trying to make a three dimensional mesh fails. The MaxCellMeasure seems to have been ignored. So this approach goes further but I am not getting the 3D mesh I need for finite element work. Any ideas?

It seems like the easy thing to do would be to convert the GraphicsComplex into a MeshRegion, but the problem is that ParametricPlot3D makes Polygons with four vertices, and those are often detected to be non-coplanar. — Jason B., Jan 04 '17 at 15:34
But you can use RunnyKine's workaround here to get a MeshRegion out of this: DiscretizeGraphics[ Normal[Show[p1, p2, p3, PlotRange -> All] /. (Lighting -> _) :> Lighting -> Automatic]] — Jason B., Jan 04 '17 at 15:40
@J.M. Thank you yes. But I did not see a way of making a good quality mesh to work with the finite element method. — Hugh, Jan 05 '17 at 19:00

score 3 · Answer 1 · answered Jun 01 '22 at 12:30

You could use the same approach as advocated in this answer:

Needs["NDSolve`FEM`"]
showmaze = 
  Uncompress[
   FromCharacterCode @@ 
    ImageData[Import["https://i.stack.imgur.com/XVJcP.png"], 
     "Byte"]];
prims = Cases[showmaze, _Cylinder | _Ball, Infinity];
prims = prims /. {{5., 5., 5.} -> {5.5, 5., 5.}, {1., 1., 1.} -> {1., 
      0.5, 1.}};
Graphics3D[prims, Boxed -> False]

ToBoundaryMesh[RegionUnion[prims]]["Wireframe"]

FEM Mesh for pipes and tubes

1 Answers1