Simplifying an equation into a certain form

Question

I have the following expression in Mathematica:

$$\beta^{\frac{1}{(1 - \beta)}} - \beta^{\frac{\beta}{(1 - \beta)}}$$

I want to express it as

$$\beta^{\frac{\beta}{(1 - \beta)}}\left (\beta -1 \right)$$

I tried Factor and Simplify without success.

I would appreciate any advise.

score 6 · Answer 1 · edited Apr 13 '17 at 12:55

6

expr = b^(1/(1 - b)) - b^(b/(1 - b));

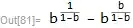
Mathematica graphics

FullSimplify[expr,ComplexityFunction -> (Count[#, Power[_, _?Negative], Infinity] &)]

Mathematica graphics

edited Apr 13 '17 at 12:55

Community

answered Jan 06 '17 at 12:12

Nasser

How come this only works with Negative power, even when ?Negative isn't used, when an expression with positive power clearly exists. – Feyre Jan 06 '17 at 12:50
Thanks. It works well, but I don't quite understand the logic behind this. I would have to read the reference that you left. – John Shin Jan 06 '17 at 13:24

score 2 · Answer 2 · answered Jan 06 '17 at 12:06

2

You can use

Simplify[Simplify[b^(1/(1-b))-b^(b/(1-b))/.b->(a-1)/a]/.a->1/(1-b)]
(*(b-1)b^(b/(1-b))*)

where $b=\beta$.

answered Jan 06 '17 at 12:06

1

More simply Simplify[expr /. b -> a + 1] /. a -> b - 1 – Simon Woods Jan 06 '17 at 21:53
@SimonWoods yeah, good catch! I just took a to be the exponent of b, but your solution does the trick too, and it's much cleaner! – AccidentalFourierTransform Jan 06 '17 at 21:58

2 Answers2