12

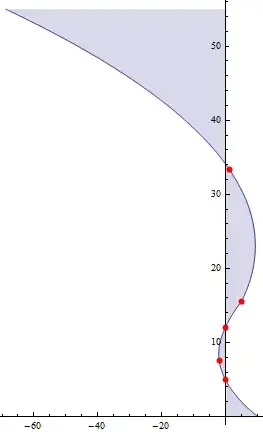
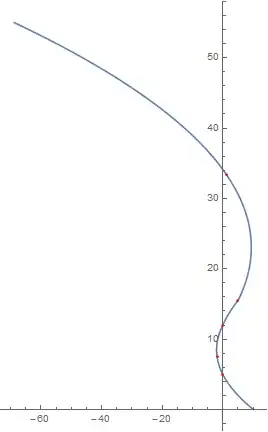
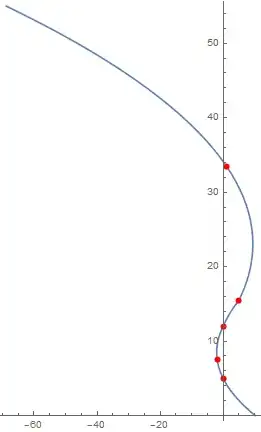
I have a such graphic:

data = {{0, 5}, {1.9, 7.5}, {0, 12}, {-5, 15.5}, {-1.2, 33.4}};
p=Plot[Interpolation[Reverse /@ data, x, InterpolationOrder -> 2], {x, 
  0, 55}, Epilog -> {Red, PointSize[.01], Point[Reverse /@ data]}]

But acutually this picture is expected(except that ticks label rotated)

Note the interpolation method should be used,but not the fit method here.How to get such graphic?

Update:

I get a lot solution in following answers.But I realize if I have a option Filling -> Axis in my p.All solution cannot work anymore.

Community
  • 1
yode
  • 26,686
  • 4
  • 62
  • 167

4 Answers4

14
p = Plot[Interpolation[Reverse /@ data, x, InterpolationOrder -> 2], {x, 0, 55}, 
         Epilog -> {Red, PointSize[.01], Point[Reverse /@ data]}, Filling -> Axis]

You can post-process p to rotate the graphics primitives:

Show[Normal[p] /. prim : _Line | _Point | _Polygon :> 
   GeometricTransformation[prim, RotationTransform[Pi/2]], 
 PlotRange -> All, AspectRatio -> GoldenRatio]

Mathematica graphics

kglr
  • 394,356
  • 18
  • 477
  • 896
  • Congratulation for 100K. :) And I realize if we have a option Filling -> Axis in p.The rotate graphic cannot include anymore? – yode Jan 14 '17 at 23:35
  • Thank you @yode. Please the new version to deal with Filling. – kglr Jan 15 '17 at 01:52
9

This is pretty neat:

data = {{0, 5}, {1.9, 7.5}, {0, 12}, {-5, 15.5}, {-1.2, 33.4}};
iFun = Interpolation[Reverse[data, 2], InterpolationOrder -> 2];
ParametricPlot[Cross[{x, iFun[x]}], {x, 0, 55}, AspectRatio -> GoldenRatio, 
               Epilog -> {Directive[Red, PointSize[.01]],
                          Point[Cross /@ Reverse[data, 2]]}]

rotated plot

I'll leave fiddling with the ticks up to you.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
6
data = {{0, 5}, {1.9, 7.5}, {0, 12}, {-5, 15.5}, {-1.2, 33.4}};
plot = Plot[
   Interpolation[Reverse /@ data, x, InterpolationOrder -> 2], {x, 0, 
    55}, Epilog -> {Red, PointSize[.01], Point[Reverse /@ data]}];


Graphics[
   Rotate[{#, Epilog /. {##2}}, Pi/2, {0, 0}], 
   AspectRatio -> GoldenRatio, Axes -> True
] & @@ plot

enter image description here

Kuba
  • 136,707
  • 13
  • 279
  • 740
4

For your updated example:

data = {{0, 5}, {1.9, 7.5}, {0, 12}, {-5, 15.5}, {-1.2, 33.4}};

p = Plot[Interpolation[Reverse /@ data, x, InterpolationOrder -> 2], {x, 0, 55}, 
  Epilog -> {Red, PointSize[.01], Point[Reverse /@ data]}, Filling -> Axis]

A variation of axisFlip from How can I transpose x and y axis on a Plot? and Plot time along the y-axis?

axisRotate = # /. {x_Point | x_Line | x_GraphicsComplex :> 
      MapAt[(#.{{0, 1}, {-1, 0}}) &, x, 1]} &;

Show[axisRotate@p, AspectRatio -> GoldenRatio/1, PlotRange -> All]

enter image description here

Tick labels still show negative values however. If we are going to fiddle with tick labels another approach opens up: just counter-rotate the labels:

rR = {#, Rotate[#, -90 °]} &;

Show[p, Ticks -> {rR /@ Range[10, 50, 10], rR /@ Range[20, 60, 20]}] // 
 Rotate[#, 90 °] &

enter image description here

This is not as nice for further processing and use so I favor the first method.

Community
  • 1
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • 1
    An alternative is to use GeometricTransformation, as in: p /. Graphics[g_, r___] :> Graphics[GeometricTransformation[g, RotationTransform[Pi/2]], PlotRange -> All, AspectRatio -> GoldenRatio, r] – Carl Woll Jan 15 '17 at 00:38
  • @CarlWoll That certainly could be useful for more complicated transformations, but is there any advantage in this case over Dot? – Mr.Wizard Jan 15 '17 at 00:39
  • 1
    It is useful because you don't have to have consider every possible Graphics primitive, e.g., Arrow, Polygon, etc. The OP example only has Point and Line, so using explicit rules for these objects works just as well. – Carl Woll Jan 15 '17 at 00:53
  • @CarlWoll I overlooked that part of your code entirely. Thanks! – Mr.Wizard Jan 15 '17 at 00:55
  • @CarlWoll Your method misses the Epilog graphics which is undesirable for the example at hand. What solution do you propose for that? One could target Epilog expressly but I wonder if there is a more general way in the spirit of that replacement rule. – Mr.Wizard Jan 15 '17 at 16:00
  • Yes, just target Epilog/Prolog as well. – Carl Woll Jan 15 '17 at 18:14
  • Alternatively, one could first use FullGraphics to move the Epilog/Prolog options into the primitives argument. – Carl Woll Jan 15 '17 at 18:46
  • @CarlWoll Since you bring it up, would you perhaps be willing to answer http://mathematica.stackexchange.com/q/83648/121? I would really like to know if there is a plan for that function, official or otherwise. – Mr.Wizard Jan 16 '17 at 04:18