Define a function $g$ as follows:
f = 2/((x1 + Sqrt[3] x2)^2 + (y1 + Sqrt[3] y2)^2)
X = vx1^2*D[D[f, x1], x1] + vx2^2*D[D[f, x2], x2] + 2 vx1*vx2*D[D[f, x1], x2]
Y= vx1*D[f, x1] + vx2*D[f, x2]
g=X+Y^2
The function $g$ is clearly a function in 6 variables ($vx1,vx2,x1,x2,y1,y2$).
Now I want to define a function in two variables $max$ as the maximum of $g$ for $x1,x2,y1,y2$ which vary in the following hypersurface
H = ImplicitRegion[{3 (-x1^2 - y1^2 + x2^2 + y2^2) +
2 Sqrt[3] (x1*x2 + y1*y2) == 0}, {x1, y1, x2, y2}]
So I want to (but I don't know how to) define the function $max:\mathbb{R}^2\rightarrow \mathbb{R}$ as follows:
$$max(vx1,vx2)=\max\limits_{(x1,x2,y1,y2)\in H}g(vx1,vx2,x1,x2,y1,y2)$$
All I could think of is the command
FindMaximum[{g, {x1, y1, x2, y2} ∈ H}, {x1, y1, x2, y2}]
but this doesn't define a function, it just gives the maximum of $g$ for specific values of $vx1,vx2$.
How can I define the function $max$? It's important to me to define it as a function because I need to
derive it in its smooth points
plot it
define other functions which involve $max$ in their definition
How can I do it?
EDIT: I followed the suggestions of user Corey979 and defined the function max[vx1,vx2], but with FindMaximum substitued by MaxValue, since I'm interested in the maximum value (as I thought was clear in my definition). But then I'm not able to do any operation with the function max:
Any of these operations
D[max[vx1, vx2], vx1]
Plot3D[max[vx1, vx2], {vx1, -10, 10}, {vx2, -10, 10}]
FindMaximum[{max[vx1, vx2]}, {vx1, vx2}]
Will require an extremely long computational time and will give no output. Which is strange, since with my old code
f = 2/((x1 + Sqrt[3] x2)^2 + (y1 + Sqrt[3] y2)^2)
X = vx1^2*D[D[f, x1], x1] + vx2^2*D[D[f, x2], x2] + 2 vx1*vx2*D[D[f, x1], x2]
Y= vx1*D[f, x1] + vx2*D[f, x2]
g=X+Y^2
H = ImplicitRegion[{3 (-x1^2 - y1^2 + x2^2 + y2^2) +
2 Sqrt[3] (x1*x2 + y1*y2) == 0}, {x1, y1, x2, y2}]
FindMaximum[{g, {x1, y1, x2, y2} ∈ H}, {vx1,vx2,x1, y1, x2, y2}]
I was able to get the answer
{2.39111, {vx1 -> 1.55608, vx2 -> 1.96316, x1 -> 0.810245, y1 -> -0.236216, x2 -> 1.34919, y2 -> -0.463331}}
Is there a better way to define max in such a way that it will be possible to perform operations with it?
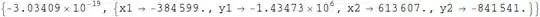
vx1andvx2? – corey979 Jan 17 '17 at 10:38Blank(_) is used when defining functions, likef[x_]:=x^2; then you call it normally withf[x]. You can't have them in expressions likeD[max[vx1_, vx2_], vx1]orFindMaximum[{max[vx1_, vx2_]}, {vx1, vx2}]. That's a simple syntax error. – corey979 Jan 17 '17 at 12:22FindMaximumas you misunderstand its output - with my def ofmax,FindMaximum[{max[vx1, vx2]}, {vx1, vx2}]makes no sense. – corey979 Jan 17 '17 at 12:28