I have a point cloud as X,Y,Z-coordinates which form a parallelepiped (with most data points inside the solid) that is rotated in space by some unknown amount and would like to find the 8 corners of it.
Basically, the answer could just be (using data.csv)
CFF[v_] := (v/{255, -255, 512})[[{3, 1, 2}]];
pts = CFF /@ Import["data.csv"];
H = ConvexHullMesh@pts
corners = MeshCoordinates@H
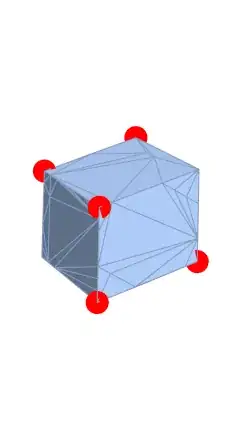
However, the mesh found by ConvexHullMesh looks like this:
As you can see, there are a number of extra mesh points that are not inside but exactly on the 6 faces, so they get treated as belonging the convex hull.
How can I simplify the mesh, ie. remove coplanar points?
Thank you for any suggestions.
I have tried TriangulateMesh, but get a very unhelpful "TriangulateMesh failed to triangulate the mesh." DiscretizeRegion crashes the kernel in 11 and fails with "DiscretizeRegion was unable to discretize the region" in 10.


TriangulateMesh[%, MaxCellMeasure -> \[Infinity]]? – Feyre Jan 19 '17 at 14:34Region\Mesh`MergeCells` may be of use per this answer – Sterling Feb 04 '21 at 08:55"The number of vertices 2 given in Polygon[{36,60}] is incorrect for \ that cell type."All in all, pretty weird.. – Sterling Feb 05 '21 at 20:47