Solving a simple equation

Question

I want to solve a simple equation

$Assumptions = 0 < v < 1 && x ∈ Reals && v ∈ Reals;
eqn1 = v == 1 - (1 - x)^(3/2)
sol = Solve[eqn1, {x},Reals]

But if I do a few more steps by hand

eqn2 = (1 - v)^(2/3) == ((1 - x)^(3/2))^(2/3) // PowerExpand
mySol = Solve[eqn2, {x}]

Did I miss some assumptions or something else? The assumtions from above don't seem to affect Solve, only the domain parameter.

I know that this is not a proof!

Plot[{x /. mySol, x /. sol}, {v, 0, 1}, PlotStyle -> {Line, Dashed}]

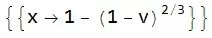
What are your assumptions on v? Mathematica assumes every variable is complex unless told otherwise. — J. M.'s missing motivation, Jan 20 '17 at 15:42
What about this Solve[eqn1, x, Reals] // ToRadicals // First? — zhk, Jan 20 '17 at 16:10

zhk · Accepted Answer · 2017-01-20T18:11:18.703

4

It seems that you just want to avoid the complex roots, so,

eqn1 = v == 1 - (1 - x)^(3/2)
sol = Solve[eqn1, x, Reals] // ToRadicals // First // Simplify // 
PowerExpand // Simplify

Normal[sol]

edited Jan 20 '17 at 18:11

answered Jan 20 '17 at 17:33

zhk

1 Answers1