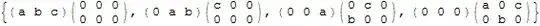Modeling Traffic flow, splitting/merging lanes with matrices

Question

I am trying to make a function that takes a list and models splitting lanes in traffic. The list below is a 1-lane road with cars a, b, and c in them, moving from left to right, and I want them to fill the available lanes to the right. {{{a,b,c}}//MatrixForm,{{0,0,0},{0,0,0}}//MatrixForm

Is there a way to define a function like that? I want something like... for one discrete timestep, have car c move into the top (left) lane. Clear[traffic]; traffic[{{a,b,c}}]:={{{0,a,b}},{{c,0,0},{0,0,0}}} and so on.

Answer 1

This is one way:

traffic[{lane_, lanes_}] := Block[{newlanes, free},
  {free} = FirstPosition[lanes[[All, 1]], 0];
  newlanes = 
   Transpose[
    Join[{ConstantArray[0, Length@lanes]}, Most[Transpose[lanes]]]];
  newlanes[[free, 1]] = lane[[-1]];
  {Prepend[Most[lane], 0], newlanes}
  ]

free finds the first available lane from the top, then the single lane and mulitple lanes are updated. Note I've assumed a single incoming lane, but the multiple lanes can be any rectangular matrix. The flow in the OP can be produced by

NestList[traffic, {{a, b, c}, {{0, 0, 0}, {0, 0, 0}}}, 3]

Please let me know if you also want the incoming lane to possibly be multi-laned.

Answer 2

xx = Partition[Insert[{a, b, c}, 0, List /@ {2, 2, -1}], 2];

Table[Row[ MatrixForm /@ {List@ArrayPad[{a, b, c}, {i, -i}], 
    ArrayPad[Transpose[xx], {{0}, {i - 3, 3 - i}}]}], {i, 0, 3}]

Answer 3

Update

The code I first posted seemed way too long for this operation so I tried again. I chose to use a different format to simplify my construction.

f[in_?VectorQ] := {in, {0, 0} & /@ in}

f[{{a__, b_}, {m__, _}}] := {{0, a}, {If[{m}[[1, 1]] === 0, {b, 0}, {0, b}], m}}

format[{v_, m_}] := Row[MatrixForm /@ {{v}, m\[Transpose]}]

Use:

format /@ Rest @ NestList[f, {a, b, c}, 4]

---

Old code

My interpretation of what you want. More verbose than I like but I found it an interesting problem.

f1[x_][ls_] := FoldList[ArrayPad[#, {x, -x}] &, ls, ls]

f2[in_] := Total @ Partition[DiagonalMatrix @ in, 2, 2, 1, 0]

f3[in_] := {f1[1][in], Reverse[f1[-1] /@ f2[in]\[Transpose]]}\[Transpose]

format[{in_, out_}] := Row[MatrixForm /@ {{in}, out}]

Use:

f3[{a, b, c}]

format /@ %

{{{a, b, c}, {{0, 0, 0}, {0, 0, 0}}},
 {{0, a, b}, {{c, 0, 0}, {0, 0, 0}}},
 {{0, 0, a}, {{0, c, 0}, {b, 0, 0}}},
 {{0, 0, 0}, {{a, 0, c}, {0, b, 0}}}}