How to plot volumes with Plot3D?

Question

A solid lies between planes perpendicular to the​ y-axis at $y=0$ and $y=1$. The​ cross-sections perpendicular to the​ x-axis are circular disks with diameters running from the​ $y=1$ to the parabola $x=\sqrt{19}y^2$. Find the volume of the solid. $$$$After evaluating the volume of the solid I wanted to make a 3D plot of this object. Since I am new to mathematica, the way I thought about it was:

    f[x_] := Integrate[Pi/4*(1 - Sqrt[x]/19^(1/4))^2, x]
    Plot3D[f[x], {x, 0, Sqrt[19]}, {y, 0, 1}]

However, I get error that state:

    Integrate::ilim: Invalid integration variable or limit(s) in 0.0003116612744631582`. >>
    Integrate::ilim: Invalid integration variable or limit(s) in 0.31166158581308273`. >>
    Integrate::ilim: Invalid integration variable or limit(s) in 0.6230115103517023`. >>
General::stop: Further output of Integrate::ilim will be suppressed during this calculation. >>

How can I fix this?

(I want to show the volume between the two curves such that the cross sections perpendicular to the x-axis are disks whose diameter run from $y=1$ to $f(x)$)

Answer 1

Update 2

Now understanding the desired region, the volume can be obtained by 'sliding' the disks onto x-axis and using cylindrical coordinates:

f[x_]:= Sqrt[x/Sqrt[19]]
vol=Integrate[r, {u,0,2Pi},{v,0,Sqrt[19]},{r,0,(1-f[x])/2}]

Surface enclosing desired volume $\frac{\sqrt{19}\pi}{24}$:

g[r_, u_, v_] := {u, r Cos[v], (1 + f[u])/2 + r Sin[v]}
ParametricPlot3D[
 g[(1 - f[u])/2, u, v], {u, 0, Sqrt[19]}, {v, 0, 2 Pi}, Mesh -> False,
  Background -> Black, AxesStyle -> White]

or using RegionPlot3D:

RegionPlot3D[
 0 < (y^2 + (z - (1 + f[x])/2)^2) <= (1 - f[x])^2/4, {x, 0, 
  Sqrt[19]}, {y, -1/2, 1/2}, {z, 0, 1}, Mesh -> None, 
 BoxRatios -> Automatic, Background -> Black, 
 AxesStyle -> Directive[Bold, White, 12
   ]]

Update

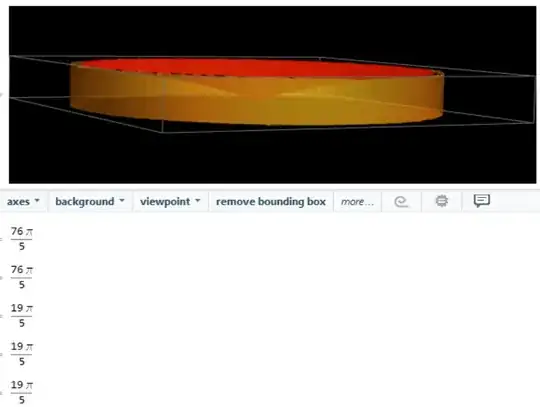
Based on OP comment below. In the following three approaches are used. The first determine the volume of the "yellow" region and the desired "red" region is determined by subtracting from bounding cylinder (volume:$19\pi$): firstly cartesian then cylindrical coordinates. The third just "flips" the region and determines directly using cylindrical coordinates.

Note: the region functionality had difficulty determining volume or even discretizing region. Others may have better approach.

region = ImplicitRegion[
   0 < x^2 + y^2 < 19 && 
    0 < z^4 < ((x^2 + y^2)/19), {{x, -Sqrt[19], 
     Sqrt[19]}, {y, -Sqrt[19], Sqrt[19]}, {z, 0, 1}}];
complement = 
  ImplicitRegion[
   0 < x^2 + y^2 < 19 && 
    0 < ((x^2 + y^2)/19) < z^4 < 1, {{x, -Sqrt[19], 
     Sqrt[19]}, {y, -Sqrt[19], Sqrt[19]}, {z, 0, 1}}];
Show[
 RegionPlot3D[complement, PlotPoints -> 40, 
  PlotStyle -> Directive[Red, Opacity[0.5]]],
 RegionPlot3D[region, PlotPoints -> 40, PlotStyle -> Opacity[0.5]],
 Background -> Black

 ]
vr = Integrate[((x^2 + y^2)/19)^(1/4), {x, y} \[Element] 
   Disk[{0, 0}, Sqrt[19]]]
cc = Integrate[
  r, {t, 0, 2 Pi}, {r, 0 , Sqrt[19]}, {z, 0, Sqrt[r/Sqrt[19]]}]
ans1 = 19 Pi - vr
ans2 = 19 Pi - cc
ans3 = Integrate[
  r, {t, 0, 2 Pi}, {r, 0 , Sqrt[19]}, {z, 0, 1 - Sqrt[r/Sqrt[19]]}]

Original Answer

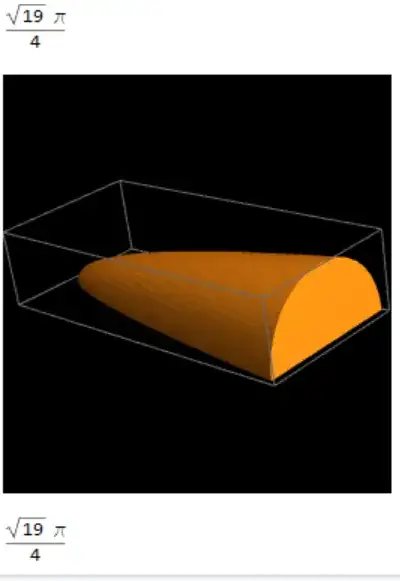
I am not sure whether the following or its complement is desired. The following is based on sections as "circular disks". If the full paraboloid is desired then double. Note can also use volume of paraboloid: $V_\text{paraboloid}= \pi a^2 h/2$ ( $a=1$,$h=\sqrt{19}$, $\mapsto \sqrt{19}\pi/2$ ):

Cylindrical coordinates:

Integrate[r, {t, 0, Pi}, {r, 0, 1}, {z, 0, Sqrt[19] r^2}]

Implicit region:

reg = ImplicitRegion[
   0 < (y^2 + z^2) < 
    x/Sqrt[19], {{x, 0, Sqrt[19]}, {y, 0, 1}, {z, -1, 1}}];
RegionPlot3D[reg, BoxRatios -> Automatic, Background -> Black]
Volume[reg]