The roots $x_{1}$ and $x_{2}$ of
$$ax^{2}+bx+c=0 $$
satisfy
$$ x_{1}+x_{2}=\frac{-b}{a} $$ and $$x_{1}x_{2}=\frac{c}{a}$$
I need Mathematica to give me $x_{1} ^ n + x_{2}^ n$ for any $n$; that is:
$${x_{1}}^{2}+{x_{2}}^{2}=(x_{1}+x_{2})^{2} -2x_{1}x_{2} = \frac{b^2-2ac}{a^2}$$
$${x_{1}}^{3}+{x_{2}}^{3}=(x_{1}+x_{2})\left ( (x_{1}+x_{2})^{2}-3x_{1}x_{2} \right )=\frac{3abc-b^3}{a^3}$$
$$\dots$$
edit: $$ {x_{1}}^{2}+{x_{2}}^{2}=\underset{\text{I also need this in all cases}}{{(x_{1}+x_{2})^{2} -2x_{1}x_{2}}} = \frac{b^2-2ac}{a^2} $$
I need $x_{1} ^ n + x_{2}^ n$ for any $n$ In terms of (Or as a function of) $$ x_{1}+x_{2} $$ and $$x_{1}x_{2}$$
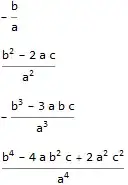
{x1, x2} = x /. Solve[a x^2 + b x + c == 0, x]; f[n_] := Together@FullSimplify[x1^n + x2^n]; f[15]– corey979 Jan 24 '17 at 00:13