I have this graph:
g=Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9,
10}, {SparseArray[Automatic, {10, 10},
0, {1, {{0, 2, 5, 7, 9, 11, 13, 15, 16, 18,
20}, {{3}, {4}, {1}, {6}, {8}, {5}, {9}, {2}, {9}, {2}, {6},
{3}, {5}, {7}, {8}, {4},
{1}, {8}, {1}, {3}}}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1}}], Null}, {VertexLabels -> {"Name"}}]
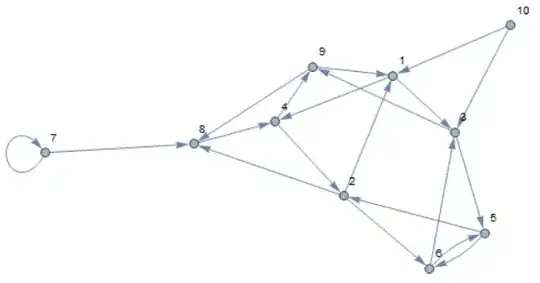
I want to find a longest path, which contains as many vertices as this path $7\to8\to4\to9\to1\to3\to5\to2\to6$ found by visual inspection. But how do I find it with Mathematica?