Graphics generation problem: how to find a curve that fits some points?

Question

I have this code:

coords = {{{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0.5, 0.1}, {1.1, 
         0.5}, {0.5, 1.1}, {0.1, 0.5}, {0.6, 0.6}}};
nnodes = Flatten[coords, 1];
l1 = {{0, 0}, {0.5, 0.1}, {1, 0}};
l2 = {{1, 0}, {1.1, 0.5}, {1, 1}};
l3 = {{1, 1}, {0.5, 1.1}, {0, 1}};
l4 = {{0, 1}, {0.1, 0.5}, {0, 0}};
meshvis = Graphics[BezierCurve[{l1, l2, l3, l4}, SplineDegree -> 2]];
nodevis = Graphics[{Black, PointSize[Medium], Point[nnodes]}];
nodenumb = Graphics[{MapIndexed[Text[#2[[1]], #1, {2, 2}] &, nnodes],{Black,Point[nnodes]}}];
defel = Show[meshvis, nodevis, nodenumb]

Which generetes the following figure:

This result is not what i want. I need the curve passes through all points(except through point 9). Any suggestions on how to approach this?

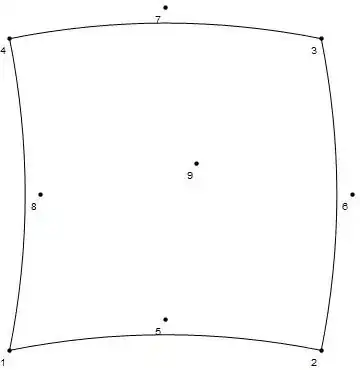
Primarily, the problem is due to your use of BezierCurve[]; recall that it only passes through the first and last points, and treats the points in between as "control points". For interpolating B-splines, see this. — J. M.'s missing motivation, Jan 27 '17 at 03:40

score 6 · Accepted Answer · edited Jan 26 '17 at 21:06

You could try the following using the fact that 3 points define a unique parabola. Must fit in the x and y directions separately.

coords = {{{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0.5, 0.1}, {1.1, 
 0.5}, {0.5, 1.1}, {0.1, 0.5}, {0.6, 0.6}}};
xcurves = Fit[coords[[1, #]], {1, x, x^2}, x] & /@ {{1, 5, 2}, {4, 7, 3}}
ycurves=Fit[Reverse/@coords[[1,#]],{1,y,y^2},y]&/@{{1,8,4},{2,6,3}}
Show[Graphics[{PointSize[0.02],Point/@coords}],Plot[xcurves,{x,0,1},PlotStyle->Blue],ContourPlot[{x==First@ycurves,x==Last@ycurves},{x,0,1.2},{y,0,1},ContourStyle->Blue]]

Graphics generation problem: how to find a curve that fits some points?

1 Answers1