How to solve two different ode system which is related?

Question

I need help on solving two systems which are related to each other. Basically, first I have to solve a non-linear ODE system. Then, I have to solve another system of equations, I have to ask mathematica to get the values from first system, in order to solve the second system.

The first system is this one:

inf = 50;
s = ParametricNDSolve[{H'[η] == -2*F[η] - ((1 - n)/(1 + n))*η*F'[η], 
    F[η]^2 - (G[η] + 1)^2 + (H[η] + ((1 - n)/(1 + n))*η*F[η])*F'[η] == 
    (F'[η]^2 + G'[η]^2)^((n - 1)/2)*F''[η] + F'[η]*((n - 1)*(F'[η]^2 + G'[η]^2)^((n - 3)/2)
    *(F'[η]*F''[η] + G'[η]*G''[η])), 
    2*F[η]*(G[η] + 1) + (H[η] + ((1 - n)/(1 + n))*η*F[η])*G'[η] == 
    (F'[η]^2 + G'[η]^2)^((n - 1)/2)*G''[η] + G'[η]*((n - 1)*(F'[η]^2 + G'[η]^2)^((n - 3)/2)
    *(F'[η]*F''[η] + G'[η]*G''[η])), 
    F[0] == 0, G[0] == 0, H[0] == 0, 
    F'[inf] == H[inf] F[inf], G'[inf] == H[inf] (G[inf] + 1)}, 
    {F, G, H, F', G'}, {η, 0, inf}, {n, Fp0, Gp0}, 
    Method -> {"Shooting", "StartingInitialConditions" -> 
    {F[0] == 0, G[0] == 0, H[0] == 0, F'[0] == Fp0, G'[0] == Gp0}}];

The value of F[η], G[η] and H[η] that I get from the first system will be used to solve the second system.

I believe there is a lot of mistakes i've done to solve the second question. Hence, I need help. thank you :)

This is the second system:

inf = 20; 
    alphabar=1;
    betabar=1;
    omegabar=0;
    R=1;
    sol =First@ NDSolve[{y1'[\[Eta]] == y2[\[Eta]] , 
y2'[\[Eta]]==(1/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*(H[\[Eta]]-((n - 1)*(F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 3)/2)*(F'[\[Eta]]*F''[\[Eta]] + 
                G'[\[Eta]]*G''[\[Eta]])))*y2[\[Eta]]+(1/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*(\[ImaginaryI]*R*(alphabar*F[\[Eta]]+betabar*G[\[Eta]]-omegabar)+F[\[Eta]])*y1[\[Eta]]-(2/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*(G[\[Eta]]+1)*y5[\[Eta]]+(R/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*F'[\[Eta]]*y3[\[Eta]]+\[ImaginaryI]*(R/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*alphabar*y4[\[Eta]],
y3'[\[Eta]]==-(\[ImaginaryI]*alphabar*(1/R))*y1[\[Eta]]-\[ImaginaryI]*betabar*y5[\[Eta]],
y4'[\[Eta]]==-((\[ImaginaryI]*R*(alphabar*F[\[Eta]]+betabar*G[\[Eta]]-omegabar)+H'[\[Eta]])/R)*y3[\[Eta]]-(H[\[Eta]]/R)*(-\[ImaginaryI]((alphabar*(1/R))*y1[\[Eta]]-\[ImaginaryI]*betabar*y5[\[Eta]]))-(1/R)*(((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2))*y3''[\[Eta]]+y3'[\[Eta]]*(n - 1)((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 3)/2))(F'[\[Eta]]* F''[\[Eta]]+ G'[\[Eta]]*G''[\[Eta]])),
y5'[\[Eta]]==y6[\[Eta]],
y6'[\[Eta]]==(1/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*(H[\[Eta]]-((n - 1)*(F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 3)/2)*(F'[\[Eta]]*F''[\[Eta]] + 
                G'[\[Eta]]*G''[\[Eta]])))*y6[\[Eta]]+(1/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*(\[ImaginaryI]*R*(alphabar*F[\[Eta]]+betabar*G[\[Eta]]-omegabar)+F[\[Eta]])*y5[\[Eta]]-(2/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*(G[\[Eta]]+1)*y1[\[Eta]]+(R/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*F'[\[Eta]]*y3[\[Eta]]+\[ImaginaryI]*(R/((F'[\[Eta]]^2 + G'[\[Eta]]^2)^((n - 1)/2)))*betabar*y4[\[Eta]],  y1[0] == 0, y2[0] == 0, y3[0] == 0, y4[0] == 0, y5[0] == 0, y6[0] == 0,y1[inf] == 0, y2[inf] == 0, y3[inf] == 0,y4[inf] == 0, y5[inf] == 0, y6[inf] == 0} /. n -> 1.0,
        {y1,y2,y3,y4,y5,y6}, {\[Eta], 0.00001, inf}];

This is the error:

 NDSolve
:Derivative order  1.  in term  y1
(1.)
[η]  should be a non-negative machine-sized integer.

Thank you so much if anyone can help me on this.

Attached is the system:

I replaced η with y, U with F, V with G and W with H.

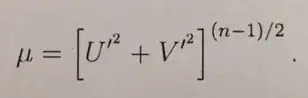
Because all but the third ODE in the second block of code are first order, there should be only seven boundary conditions, not twelve. Please specify which you wish to use. Also, the fourth ODE contains y3''[η] as well as y4'[η]. Is this correct? — bbgodfrey, Feb 03 '17 at 10:23
Also, since these equations are linear and homogeneous in y the solution is zero. — bbgodfrey, Feb 03 '17 at 11:23
I would like to see the literature of the two systems. Is there any? — zhk, Feb 03 '17 at 15:17
I have attached the original questions. I understand what u said, there should be 7 boundary conditions. But how should i choose? @bbgodfrey — dayana nisa, Feb 06 '17 at 01:25
Your y4'[η] Mathematica equation contains y3''[η] but the corresponding equation shown in the image does not. Please check your code carefully for such errors. Also, the set of six ODEs is linear in y. With y[0] == 0 for the six boundary conditions, the only solution is y == 0 everywhere. — bbgodfrey, Feb 06 '17 at 07:19
As you can see from the attached picture (the last term of y4'[η]), there is D{μ*something here}. If you look closely, the term 'something here' is actually y3'[η](same thing). So if I have D{μ*something here} = D{μ*y3'[η]} meaning if we do product rule, we will get uv'+vu'=μ*y3''[η]+y3'[η]*μ'. That is why there exist y3''[η]. @bbgodfrey — dayana nisa, Feb 07 '17 at 01:16
Thanks for clarifying the meaning of D in the picture. It remains the case that the solution is identically zero for the given boundary conditions. — bbgodfrey, Feb 07 '17 at 01:37

zhk · Answer 1 · 2017-02-03T14:21:24.620

Here I will illustrate with a simple example to solve two couple systems of odes.

Method I

(*The first system*)
Ode1 = x'[t] == 1/y[t];    
Ode2 = y'[t] == x[t];    
ics := {x[0] == 1, y[0] == 2};
sys = Join[{Ode1, Ode2}, ics];    
soln = First@NDSolve[sys, {x, y}, {t, 0, 10}];    
x1[t_] := Evaluate[x[t] /. soln]; (*assign the interpolating function x[t] to x1[t]*)    
y1[t_] := Evaluate[y[t] /. soln]; (*assign the interpolating function y[t] to y1[t]*)    
(*The second system*) 
Ode3 = x2'[t] == x1[t];
Ode4 = y2'[t] == x2[t] + y1[t] + y2[t];
ics2 := {x2[0] == -1, y2[0] == -2};
sys1 = Join[{Ode3, Ode4}, ics2];
soln1 = First@NDSolve[sys1, {x2, y2}, {t, 0, 10}];
Plot[{x1[t], y1[t], {x2[t], y2[t]} /. soln1}, {t, 0, 10}]

Method II

Solve the two systems as one,

Ode3 = x2'[t] == x[t];    
Ode4 = y2'[t] == x2[t] + y[t] + y2[t];    
combsys12 = Join[{Ode1, Ode2, Ode3, Ode4}, ics, ics2];    
combsoln = First@NDSolve[combsys12, {x, y, x2, y2}, {t, 0, 10}];    
Plot[{x[t], y[t], x2[t], y2[t]} /. combsoln, {t, 0, 10}]

How to solve two different ode system which is related?

1 Answers1