3

I have a set of data from which I'm able to generate closed contours (surfaces) in with ListContourPlot3D. I would like to determine the (approximate) volume of these surfaces as well as their surface areas. Is this possible in some manner?

Will Bertsche
  • 31
  • 1
  • 2
    Where is the data? – zhk Feb 05 '17 at 15:43
  • This is highly dependant on the surface. Oftentimes the output from ContourPlot3D includes many polygons with 4 points which aren't quite as planar as the region functions want. – Jason B. Feb 05 '17 at 22:38

2 Answers2

2

You can use DelaunayMesh, RegionBoundary, and RegionMeasure

Points on a unit sphere for example data (Taken from:how to get $n$ equidistributed points on the unit sphere):

points = With[{points = 5000, samples = 40000, iterations = 20}, 
   Nest[With[{randoms = Join[#, RandomPoint[Sphere[], samples]]}, 
      Normalize@Mean@randoms[[#]] & /@ 
       Values@PositionIndex@Nearest[#, randoms]] &, 
    RandomPoint[Sphere[], points], iterations]];

Calculating volume and surface area:

ListContourPlot3D[points, Contours -> {0}]
object = DelaunayMesh[points];
objectSurface = RegionBoundary[object];

RegionMeasure[object, 3]
RegionMeasure[objectSurface, 2]

4.18349

12.5579

Community
  • 1
Young
  • 7,495
  • 1
  • 20
  • 45
2

You can use BoundaryDiscretizeGraphics to convert the contour plot to a BoundaryMeshRegion, then measure the volume and surface area of the region.

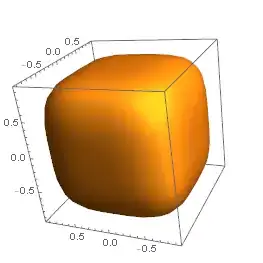
data = Table[x^4 + y^4 + z^4, {x, -1, 1, 0.2}, {y, -1, 1, 0.2}, {z, -1, 1, 0.2}];

g = ListContourPlot3D[data, Contours -> {0.8}, 
  DataRange -> {{-1, 1}, {-1, 1}, {-1, 1}}, Mesh -> None]

enter image description here

b = BoundaryDiscretizeGraphics[g]

enter image description here

RegionMeasure /@ {b, RegionBoundary[b]}
(* {5.2023, 15.2752} *)
Simon Woods
  • 84,945
  • 8
  • 175
  • 324