How do we solve N-Rooks variation using primes?

Question

Using a $p_n $x $p_n$ matrix, how can we solve the N-Rooks problem to find a prime in every row and column?

Table[MatrixForm[Table[If[PrimeQ[n], "P", "."], {m, 0, Prime[o]^2 - Prime[o], 
Prime[o]}, {n, m + 1, m + Prime[o]}]], {o, 1, 8}]

Here is the $11 $x$11$ matrix with the possible prime positions for the queens:

N-RooksPrimeVariation

Note: single primes are always in the $p$-th column.

This is one possible solution (done by hand):

N-RooksPrimeSolution

Edit Changed the title and link as Paxinum suggested.
OEIS A215637 has these counts of multiple solutions through $10th$ prime:
$$ 1, 1, 1, 2, 7, 72, 2144, 2641, 1345721, 2191254096$$

I think you need to qualify the question a bit more... What is the equivalent condition of "two queens not attacking each other"? — rm -rf, Oct 27 '12 at 02:53
Ah, I see. So your 11x11 was the set of all possible positions then... — rm -rf, Oct 27 '12 at 03:13
@rm-rf, yes, All we need to do is circle one prime in each row and each column. In this example, we would have 11 circles. — Fred Daniel Kline, Oct 27 '12 at 03:19
Then this is not an $n$-queen problem, but an $n$-rook problem... — Per Alexandersson, Oct 28 '12 at 09:08
@Paxinum, yes that is almost it. Unlike either problem, we can't move the pieces around. We must use what is available and remove what we don't need. — Fred Daniel Kline, Oct 28 '12 at 09:30

user1066 · Answer 1 · 2016-08-19T09:50:04.800

Another possibility, at least for relatively small matrices, is to take the determinant (strictly speaking it is the permanent that is required, I suppose).

For example, for an $11 \times 11$ matrix (o=5), I find there are 7 solutions.

primePositions5 = 
  Position[With[{o = 5}, 
    Table[If[PrimeQ[n], 1, 0], {m, 0, Prime[o]^2 - Prime[o], 
      Prime[o]}, {n, m + 1, m + Prime[o]}]], 1];

mylist = List @@ (Det@
     SparseArray[## -> Subscript[a, ##] & /@ 
       primePositions5] /. {-x_ -> x})

gives the following:

enter image description here

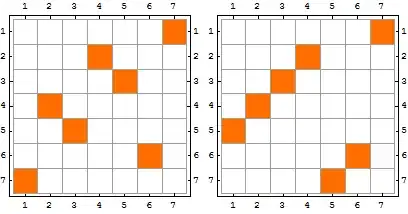
Matrix plots of all seven solutions:

MatrixPlot[
   Normal@SparseArray[(List @@ #) /. 
      Subscript[a, {x_, y_}] -> {x, y} -> 1], Mesh -> All, 
   ImageSize -> 200] & /@ mylist

I'll give then as a grid:

enter image description here

I reckon it needs to be emphasized that the Mathematica's Det command is slow.

With o=7 which gives a $17 \times 17$ matrix, I obtain 2144 solutions. For 0 =8 ($19 \times 19$), the figure is 2641. I could not go beyond this with the computer I am using (with Mathematica 7, as it so happens).

For o=4 ($7 \times 7$), I get two solutions:

7x 7 matrix

Update for Mathematica 11

In Mma 11, we can use the Permanent function

myListAlt = List @@ (SparseArray[## -> Subscript[a, ##] & /@  primePositions5] // 
 Permanent // Expand)

The behaviour of Det seems to have changed somewhat since this question was posted.
I now need to Expand the result of the Det function:

mylist = List @@ (Expand@
 Det@SparseArray[## -> Subscript[a, ##] & /@ 
    primePositions5] /. {-x_ -> x})

and

mylist == myListAlt

True

FWIW: it is well-known that computing the permanent is an even more difficult task than computing the determinant... — J. M.'s missing motivation, Oct 30 '12 at 00:18
The built-in Permanent[] can be a bit slow; see here for slightly faster routines. I should also note at this point that Ilan Vardi discussed a similar problem in his book Computational Recreations in Mathematica. — J. M.'s missing motivation, Aug 19 '16 at 10:02

score 6 · Accepted Answer · edited Oct 27 '12 at 09:01

6

A very simple one, not very elegant :

f[o_] := Module[{mat, sol, vars, const, output}, 
  mat = Table[If[PrimeQ[n], Unique["p"], 0], {m, 0, Prime[o]^2 - Prime[o], 
    Prime[o]}, {n, m + 1, m + Prime[o]}];
  vars = Cases[Flatten[mat], _?(Not[NumericQ[#]] &)] ;
  const = Join[{Last[First[mat]] == 1}, Total[#] == 1 & /@ mat, 
    Total[#] == 1 & /@ Transpose[mat], 
    Thread[GreaterEqual[vars, 0]]];
  sol = FindInstance[const, vars, Integers];
  output = (mat /. First[sol])
]

f[8]/.{0 -> "."} //MatrixForm

prime

edited Oct 27 '12 at 09:01

István Zachar

47,032
20
143
291

answered Oct 27 '12 at 08:43

b.gates.you.know.what

20,103
2
43
84

Hey, could you help me understand the puzzle? – Rojo Oct 27 '12 at 08:44
I understood you want to build a matrix with "P"'s and 0's such that there is only one "P" in every row and column - some sort of simplified sudoku. – b.gates.you.know.what Oct 27 '12 at 08:46
2

But couldn't those be 1s and 0s? What's prime about this? – Rojo Oct 27 '12 at 08:47
4

The position where the 1's can be placed. – b.gates.you.know.what Oct 27 '12 at 08:47
Oh so in 9x9 matrix, 2nd row, 1st column would be 10th position so you can't put a 1 there? Sorry, 5:50AM, slept 2hs yesterday – Rojo Oct 27 '12 at 08:50
The dimension of the matrix is Prime[o], so it can never be 9x9. – b.gates.you.know.what Oct 27 '12 at 08:55
+1, very nice! I was playing around with patterns of primes and thought a sudoku type of puzzle might be possible. It seems to be computer solvable. The last row of each matrix is one of the segements from Oppermann's Conjecture $(p^2-p,p^2]$ – Fred Daniel Kline Oct 27 '12 at 09:32

Rojo · Answer 3 · 2012-10-27T18:26:01.280

This is neither elegant nor smart nor memory efficient. It is a brute force method to get all solutions of a given size

isGood[m_] := Sort@m === reye@Length@m;
i : reye[l_] := i = Reverse@IdentityMatrix@l;

getAllSolutions[n_?PrimeQ] := With[{id = IdentityMatrix@n},
     Pick[id, #, 1] & /@ Boole@PrimeQ@Partition[Range[n^2], n] // 
     Tuples]~Select~isGood;

So

Row[MatrixForm /@ #] & /@ 
  Composition[getAllSolutions, Prime]~Array~4 // 
 Column@Riffle[#, "New prime"] &

Gives

Mathematica graphics

EDIT

I imagined that a solution along the lines of @bgatessucks 's great answer, but with booleans, would be more efficient and appropriate. However, while this is true for sizes below 13 (an order of magnitude faster in my tests), for some reason it suddenly becomes terribly slow afterwards.

v2[n_?PrimeQ, nsols_Integer: 1] := Module[{mat, vars},
  {mat, {vars}} = 
   Reap[PrimeQ@Partition[Range[n^2], n] /. True :> Sow@Unique["p"]];
  SatisfiabilityInstances[
    And @@ BooleanCountingFunction[{1}, n] @@@ 
      Join[mat, Transpose@mat], vars, nsols] /. 
   res_ :> (mat /. (Thread[vars -> #] & /@ res) /. {False -> ".", 
       True -> "P"})
  ]

Now

MatrixForm /@ v2[Prime@6, 3]

Gives

Mathematica graphics

@FredDanielKline, added an edit – Rojo Oct 27 '12 at 18:26 — Rojo, Oct 27 '12 at 18:26

How do we solve N-Rooks variation using primes?

3 Answers3

Update for Mathematica 11

Linked